نظرية التشغيل الذاتي أو نظرية الآلات ذاتية التشغيل أو نظرية الآلات المجرّدة (الإنجليزية: Automata Theory) هي نظرية تهتم بتعريف و دراسة خواص الآلات الحاسوبية المجرّدة. تاريخيّا دُرست قضايا هذه النظرية كتصوّر للحساب الإلكتروني قبل ظهور الحواسيب الحديثة لكنّها أثبتت قدرتها على تمثيل العديد من العمليات الحاسوبيّة في وقتنا الحالي، و تستخدم بكثرة كأداة للبرهان الرياضي الحاسوبي، لذلك فهي تعتبر من أهمّ ركائز علوم الحاسوب النظرية و الأنظمة المنهجية.
فهرس |
آلة ذاتية التشغيل
تعتبر الآلة ذاتية التشغيل نموذجاً رياضيا للآلات المجرّدة؛ وهي آلات لها حالات مختلفة، تبدأ في حالة معيّنة ثم تنتقل من حالة إلى أخرى تبعاً لعوامل خارجيّة، تُمثَّل كسلسلة من الرموز الداخلة. يُقرأ الدخل رمزاً فرمزاً حتى تتوقف الآلة عند الانتهاء، أو عند حصول خطأ.
استعمالات النظرية
تستعمل نظرية الآلات الذاتية التشغيل في علوم الحاسوب في حلول كثيرة منها:
- تطوير برامج للتّحقق من صحة و سلامة الدّارات الرقمية.
- المحلّل المفرداتي (التركيبي) لمعظم مصرّفات لغات البرمجة؛ أي المكوّن الذي يهتمّ بتحليل وقطع النصّ الدّاخل (مصدر البرنامج) إلى وحدات منطقية؛ كأسماء المتغيرات، والأعداد والتنقيط.
- برامج لتحليل صفحات كثيرة من الإنترنت، والبحث عن كلمات معينة أو نماذج نصّية.
- برامج للتحقّق من صحّة برامج أخرى، فيما يعرف بالتحقق من النماذج (Model Checking).
مثال آلة بسيطة ذاتية التشغيل
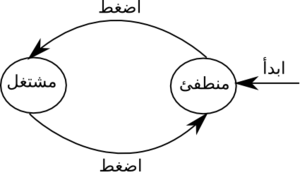
- لنفرض مثلا أننا نريد تمثيل مصباح كهربائي بسيط يمكن إطفاؤه و تشغيله بالضغط على زر إلكتروني. يمكن تمثيل حالتي المصباح المنطفئة و المشتغلة بالحالتين "منطفئ" و "مشتغل" على التّرتيب. يبقى المصباح في إحدى الحالتين حتى يقوم أحدهم بالضغط على الزر ليتحوّل المصباح إلى الحالة الأخرى.
يبين هذا الشكل الأول آلة المصباح السّابق وصفها:
تبدأ الآلة في حالة "منطفئ" و لذلك هناك السهم "ابدأ" الذي يشير لهذه الحالة. تسمّى الدوائر المرسومة حالات، جمع "حالة"، كلّ حالة تصف وضع المصباح في وقت ما. تمثل الأسهم الظاهرة ما يسمّى بالدّخل، و هذا بدوره يمثّل التأثيرات الخارجية على الآلة، فلدينا هنا رمز دخْل واحد يسمى "اضغط"، يقوم بنقل الآلة بين حالتي الانطفاء و الاشتغال.
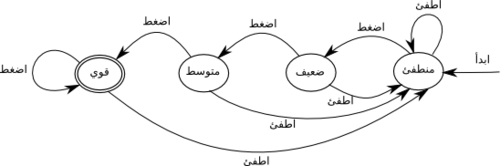
في بعض الآلات يمكن أيضا تحديد الحالات التي تنتهي عندها الآلة بنجاح، فيمكن إذن تسميتها الحالات القابلة أو النهائية. لنفرض مثلا أن لنا مصباحا آخر متطوّرا له ثلاث حالات للتشغيل: "ضعيف"، "متوسّط" و "قويّ"، و لدينا أيضا زرين: أحدهما يقوم بإطفاء المصباح دائما فنسمي هذه العملية "أطفئ"، و الآخر يزيد من شدّة المصباح فنسمّي تأثيره "اضغط". ينتقل المصباح بين حالات شدّة الضوء المختلفة بإرسال عمليّة "اضغط".
إذا أردنا جعل هدفنا هو تشغيل المصباح إلى أقصى قوة يمكن تمثيله بالشّكل التّالي:
تمثّل الدائرة المضاعفة الحالة النهائية للآلة. تقبل هذه الآلة سلاسل الدّخل الآتية:
- اضغط-اضغط-اضغط
- أطفئ-اضغط-اضغط-اضغط-اضغط
- اضغط-اضغط-اضغط-أطفئ-اضغط-اضغط-اضغط
لأنها تنتهي كلها عند الحالة النهائية. لكنها لا تقبل السلاسل التالية:
- اضغط-اضغط-اضغط-أطفئ
- اضغط-أطفئ-اضغط-اضغط
لأنها تنتهي عند حالات غير نهائية.
التعريف الرياضي للآلات الذاتية التشغيل
أولا سنقوم بتعريف الآلة الذاتية التشغيل المحدّدة، و هي الآلة التي تكون دائما في حالة واحدة بعد قراءة أي رمز دخْل معيّن، وذلك لأنه عند كل حالة لا يوجد سوى نقلة واحدة لكل رمز دخْل. هناك أيضا الآلات غير المحدّدة، سيتم التفصيل في الفرق بين الإثنين في الأقسام التالية.
تعرّف الآلة الذاتية التشغيل المحدّدة A رياضيات بأنها خماسية  بحيث أن:
بحيث أن:
- Q هي مجموعة محدودة من الحالات.
- Σ هي مجموعة محدودة من رموز الدخْل.
- δ هي دالة للنقل (أو التحول) معرفة بـ
 ، يكون مدخلها ثنائية من حالة (q) و رمز دخل (a)، و مخرجها حالة (
، يكون مدخلها ثنائية من حالة (q) و رمز دخل (a)، و مخرجها حالة ( )، أي
)، أي  .
. - q0 هي حالة البدأ التي يبدأ منها التشغيل، و هي تنتمي إلى المجموعة Q.
- F هي مجموعة من الحالات النهائية، وهي مجموعة محتواة في Q.
مثال المصباح المتقدم
في مثال المصباح المتقدّم السابق لدينا:
- مجموعة الحالات Q هي {منطفئ، ضعيف، متوسط، قوي}.
- مجموع رموز الدخل Σ هي {أطفئ، اضغط}.
- تم تمثيل الدالة δ في الشكل السابق بالأسهم التي تنتقل من حالة إلى أخرى، و يمكن تعداد هذه الدالّة:
- (منطفئ، أطفئ)
 منطفئ
منطفئ - (منطفئ، اضغط)
 ضعيف
ضعيف - (ضعيف، أطفئ)
 منطفئ
منطفئ - (ضعيف، اضغط)
 متوسط
متوسط - (متوسط، أطفئ)
 منطفئ
منطفئ - (متوسط، اضغط)
 قوي
قوي - (قوي، أطفئ)
 منطفئ
منطفئ - (قوي، اضغط)
 قوي
قوي
- (منطفئ، أطفئ)
- حالة البدء q0 هي منطفئ.
- مجموعة الحالات النهائية F هي مجموعة وحيدة العنصر و هي: {قوي}.
أنواع الآلات الذاتية التشغيل
هناك ثلاث أنواع للآلات الذاتية التشغيل:
آلات ذاتية التشغيل محددة
كما ذكرنا سابقا فإن الآلات الذاتية التشغيل المحدّدة (بالإنجليزية Determinisic Finite State Automaton أو باختصار DFA) تكون دائما في حالة واحدة فقط مهما كانت سلسلة الدخل التي قامت بتصريفها، و ذلك لأنه لا توجد سوى نقلة واحدة لكل رمز دخل عند كل حالة.
كل الأمثلة السابقة هي آلات محدّدة.
آلات ذاتية التشغيل غير محددة
الآلات غير المحدّدة (بالإنجليزية Nondeterminisic Finite State Automaton أو باختصار NFA) هي آلات يمكن أن تكون في حالات محتملة عدّة عند كل لحظة، حيث يمكن لها أن تشتغل في جهات عدّة عند كلّ رمز دخل. يتم تحديد الاتجاه المناسب خطوة بعد خطوة عند كل رمز كلما رفض اتجاه ما هذا الرمز.
تكون الآلة غير المحدّدة في حالة نهائية (أي حالة قبول) إذا كانت أي من الحالات المحتملة الحالية حالة قبول.
مثال آلة غير محدّدة
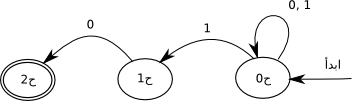
الشكل التالي يوضح آلة غبر محدّدة. لاحظ أن هذه الآلة تقبل كل السلاسل المتكونة من الأرقام 0 و 1 و المنتهية بالسلسلة 1-0 (تُقرأ السلسلة من اليمين إلى اليسار). لاحظ انه في الحالة ح0، عند إدخال الرمز 1 هناك حالتين محتملتين هما ح0 نفسها و ح1.
التعريف الرياضي
رياضيا التعريف هو نفس تعريف الآلة المحددة مع اختلاف و حيد في الدالة. الدالة δ للآلة المحددة تنتج حالة واحدة فقط عند كل ثنائية حالة و رمز، أما دالة الآلة غير المحددة فتنتج مجموعة من الحالات. يمكن استبدال العنصر الثالث في قائمة التعريف السابقة بالتعريف:
- δ هي دالّة للنقل (أو التحول) معرفة بـ
 ، يكون مدخلها ثنائية من حالة (q) و رمز دخل (a)، و مخرجها مجموعة حالات (
، يكون مدخلها ثنائية من حالة (q) و رمز دخل (a)، و مخرجها مجموعة حالات ( ) تنتمي إلى المجموعة (Q)، أي
) تنتمي إلى المجموعة (Q)، أي  .
.
يرمز  إلى مجموعة كل المجموعات التي يمكن تكوينها من عناصر المجموعة Q.
إلى مجموعة كل المجموعات التي يمكن تكوينها من عناصر المجموعة Q.
مثال الآلة غير المحددة السابق
- مجموعة الحالات Q هي { ح0 ، ح1، ح2}.
- مجموع رموز الدخل Σ هي {0، 1}.
- الدالة δ:
- (ح0، 0)
 {ح0}
{ح0} - (ح0، 1)
 {ح0, ح1}
{ح0, ح1} - (ح1، 1)
 {ح2}
{ح2}
- (ح0، 0)
- حالة البدأ q0 هي ح0.
- مجموعة الحالات النهائية F هي مجموعة وحيدة العنصر و هي: {ح2}.
آلات ذاتية التشغيل غير محددة بنقلات معدومة الرمز
بالإنجليزية Nondeterministic finite automata with ε transitions أو ε-NFA.
هذه الآلات مشابهة للآلات غير المحددة مع إمكانية تنقلها من حالة إلى أخرى من دون إدخال أي رمز. يرمز للتنقل المعدوم بـ ε. و هذا يعني أن الآلة يمكن أن تكون في مجموعة الحالات التي يمكن التنقل إليها من الحالة الحالية باستعمال هذا الرمز.
تساوي الآلات
مع أن ذلك قد لا يكون واضحا للوهلة الأولى، إلا أن جميع أنواع الآلات الذاتية التشغيل السابقة لها نفس القوة الرياضية. أي يمكن تحويل أي آلة غير محددة مثلا إلى آلة محدّدة تقبل نفس السلايل و العكس صحيح. إلا أنه عادة تكون الآلة المحدّدة أكثر تعقيدا من الأنواع الأخرى.
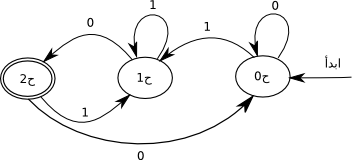
فمثلا، الآلة التالية لها نفس قوة الآلة غير المحدّدة السابقة. يمكن التحقق من ذلك بسهولة بتجريب مجموعة من السلاسل.
مراجع
- John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman (2003). Introduction to Automata Theory, Languages, and Computation.
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X.
وصلات خارجية
| فروع المعلوماتية |
الحقول الأساسية للمعلوماتية |
تحرير |
|---|---|---|
| معلوماتية نظرية | تحسيب | خوارزميات | نظرية المعلومات | نظرية الأتمتة | نظرية المخططات | نظرية التعقيد | تعمية | لغات شكلية | استمثال | بناء المترجمات البرمجية | نظرية أنظمة التشغيل | نظرية قواعد البيانات | نظرية التعمية | طريقة شكلية | تحسيب طبيعي | |
| معلوماتية عملية | أنظمة تشغيل | حوسبة | رسوميات الحاسب | قواعد بيانات | بنى بيانات | برمجة | |
| معلوماتية تقنية | تكنولوجيا المعلومات | شبكات الحاسب | عتاد الحاسب | أمن الحاسب | اختراق الحاسب | |
| معلوماتية تطبيقية | أنظمة معلومات | معلوماتية حيوية | معلوماتية جيولوجية | كيمياء حاسوبية | فيزياء حاسوبية | معلوماتية اقتصادية | وسائط متعددة | |
| ذكاء اصطناعي | تعلم آلي | معلوماتية عصبونية | طرق التصنيف | لغويات حاسوبية | |
| برمجيات | لغات البرمجة | برمجيات حرة | برمجيات تجارية | |
| أنظمة التشغيل | دوس | ويندوز | يونكس | لينكس | ماك أو إس | نتوير | تاريخ أنظمة تشغيل الحاسوب | |
| عتاد الحاسب | وحدة المعالجة المركزية | ذاكرة الحاسب | القرص الصلب | اللوحة الأم | |