جمع الأعداد طريقة لوضع شيئين أو أكثر معًا لمعرفة كم يكون المجموع.والأشياء المتشابهة وحدها هي التي تجمع. أي أنك لا تستطيع جمع تُفاح وأقلام رصاص معًا.
هَبْ أن لديك مجموعة من 5 تفاحات ومجموعة من 3 تفاحات على طاولة.
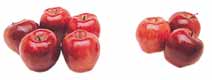 |  |
ضع الآن المجموعتين معًا في مجموعة واحدة من 8 تفاحات. | إنك تجمع عندما تضع مجموعتين أو أكثر معًا لمعرفة كم يكون المجموع. |
تَعَلُّم الجمع
لتعرف عدد الأشياء التي جمعتها لتكوين مجموعة جديدة، عليك أن تقوم بعدِّها، أو التفكير فيها معًا.
الجمع بواسطة العدّ:
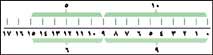
لدى خالد 3 كُريات زجاج حمراء و 4 كُريات زجاج زرقاء وضعها معًا في مجموعة واحدة.
كم كرية زجاج توجد في المجموعة الأولى؟ عُدَّها. يوجد فيها 3 كُريات. كم كرية زجاج توجد في المجموعة الثانية؟ عُدَّها. يوجد فيها 4 كريات. ضع الآن الكريات معًا في مجموعة ثالثة ثم عدها. هناك 7 كريات. نُسمي هذا
العد معًا. إنك عددت كي تعرف كم تكون 3 كريات و 4 كريات معًا. لقد اكتشفت أن 3 و 4 تكون 7.
افترض أنك رسمت 3 دوائر. ارسم الآن 4 دوائر أخرى إلى جانب الثلاث الأولى. أنت تعلم بوجود 3 دوائر مسبقًا.
لذا يُمكنك أن تفكر في 3 وتشير لكل من الدوائر الأربع الجديدة، وتعدّ :4، 5، 6، 7 . ويُسمَّى هذا
العدّ المستمر، وعن طريقه تعرف كم يكون 3 و 4 معًا بأن تفكر في 3 للمجموعة الأولى، وتأخذ في العدّ حتى تُكمل عدّ الدوائر الأربع في المجموعة الثانية. وطريقة العدّ المستمر، أسرع في جمع الأشياء من عدّها معًا.
الجمع بواسطة التفكير:
افترض أنه يوجد 4 بنات عند السبورة و 5 بنات حول طاولة القراءة. حاول أن تعرف عدد البنات الإجمالي عن طريق التفكير. مثلاً باستطاعتك التفكير ¸إنني أعلم مسبقاً أن 4 و 4 يُكون 8. لذلك 4 و5 ستزيد 1. هذا يعني أن 4 و 5 = 9 بنات. يُسمى هذا
التفكير معًا، وهو طريقة جمع أسرع من العدّ معًا، أو العدّ المستمر.
إعادة التجميع:
افترض أنك تريد أن تضع مجموعتين معًا في مجموعة جديدة، وأن المجموعة الجديدة ستكون أكثر من 10. فمثلاً، أرادت هيفاء أن تعرف كم يكون مجموع العددين 9 و6. لاكتشاف ذلك، رسمت
خط أعداد.
ثم رسمت خطين لتُبين 9 و6 كما يظهر أدناه.
وجدت هيفاء أن 9 و 6 = 15. لكنها رأت شيئاً مهماً ورسمت خطين آخرين.
وجدت هيفاء أن 9 و 6 = 10 و 5. من الأسهل للمبتدئين جمع 10 و 5 من جمع 9 و 6. نسمي تحويل المجموعتين 9 و6 إلى المجموعتين 5 و 10 إعادة تجميع. إليك بعض الأمثلة :
8 + 4 = 12 (10 + 2 )
7 + 8 = 15 ( 10 + 5 )
9 + 4 = 13 (10 + 3 ).
كتابة الجمع:
يجب عليك تدوين مسائل جمعك، ليكون لديك سجل لعدّك أو تفكيرك. تستطيع إعداد سجل باستعمال الصور:
أو باستعمال الأرقام والكلمات: 2 و 4 = 6.
لكن الأسهل والأفضل عمل سِجل باستعمال الأرقام والإشارات :
2 + 4 = 6 أو
في المثال الأول، تخبرك إشارة الجمع (+) بأن تجمع. تستطيع أن تقرأ 2 + 4 (كاثنين وأربعة). إشارة المساواة (=) تعني أن المجموعات التي في أحد طرفي الإشارة تساوي المجموعة التي في الطرف الآخر من الإشارة. تستطيع أن تقرأ 2 + 4 = 6 (كاثنين وأربعة تكوِّنان ستة). يُبين المثال الثاني كيف تكتب مسألة الجمع عندما تريد كتابة الجواب على ورقة. تُسمىَّ كل من المجموعتين أو المجموعات التي تريد وضعها معًا (أو جمعها) المضاف. المجموعة الجديدة تسمى المجموع.
حقائق الجمع:
عند وضع المجموعتين معًا، اكتشفت أن 5 + 3 = 8، 3 + 4 = 7 و 9 + 6 = 15. نُسمي تلك
حقائق جمع. تتكون كل حقيقة منها من اثنين أو أكثر من المضافات والمجموع. تستطيع اكتشاف جميع حقائق الجمع بوساطة وضع مجموعات أشياء معًا. ويتدرب بعض المبتدئين باستخدام مجموعات من قطع نقدية أو أغطية قوارير.
ومن الأفضل تعلَّم حقائق الجمع كي تستطيع استعمالها بسرعة وسهولة. وستكون قادرًا على استعمالها في حياتك اليومية. ستحتاجها أيضًا عندما تريد جمع أعداد أكبر معًا وحل مسائل.
تَعلُّم حقائق الجمع تلك يبدو مُجْهِدًا في البداية، لكن توجد طرق عدة لجعل تَعلُّم الحقائق سهلاً. على سبيل المثال، إذا نظرت لكل الحقائق التي جُمع فيها عدد مع 1، سترى أن تعلمها يُشبه العدَّ العادي. ونجد كثيرًا من الأزواج المضافة، كذلك، يكون أحدها مجرد عكس للآخر. مثلاً جمع 4+5 يساوي جمع 5 + 4نفسه. نسمي حقيقة 3 + 3 = 6 مضاعفة. ومن المفيد معرفة المضاعفات. إذا عرفت أن 4 + 4 = 8، فإن 3 + 4 يكون أقل من 8 بـ 1، و 4 + 5 يكون أكثر من 8 بـ 1. يجب أن تكون قادرًا على التفكير في طرق أخرى، لتساعدك على تعلُّم حقائق الجمع.
|
| حقائق الجمع |
|
| المضاف | في 4 + 9 = 13، العددان اللذان جُمعا، 4 و 9 كلاهما مضاف. | | حقيقة الجمع | هي عبارة أساسية في الجمع. مثلاً 2 + 3 = 5 و 8 + 7 = 15 هي حقائق جمع. | | الحَمْل | في الجمع يعني ترحيل عدد من خانة في المجموع إلى الخانة المجاورة له. العشرة في خانة الآحاد يجب أن تنقل إلى خانة العشرات. | | المجموع | في 4 + 9 = 13، الإجمالي 13 يكون هو المجموع. |
|
جمع أعداد أكبر
يمكنك استعمال حقائق الجمع وفكرة قيمة الخانة لجمع أعداد أكبر.
|
| حقائق الجمع الإحدى والثمانون |
|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | | | | | | | | | | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | | | | | | | | | | | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | | | | | | | | | | | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | | | | | | | | | | | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | | | | | | | | | | | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | | | | | | | | | | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | | | | | | | | | | | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | | | | | | | | | | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|
جمع العشرات:
أُعطي خالد الأسبوع الماضي علبتين داخل كل منهما عشر قطع من الحلوى، فيكون مُجمل ما لديه 20 قطعة حلوى. هذا الأسبوع أُعطي خالد 3 علب احتوت معًا على 30 قطعة. كم قطعة يكون مُجمل مالدى خالد؟ تستطيع أن
تعرف الجواب بوساطة العدّ. تجد أن مجمل ما لدى خالد 5 علب تحتوي على50 قطعة حلوى: تستطيع أن تعرف الجواب بواسطة الجمع.
| |
|
| 2 | علبــة | | 20 | قطعة حلوى | | 3 | علب | | 30 | قطعة حلوى | | 5 | علب | | 50 | قطعة حلوى | |
إذا عرفت أن 2 + 3 = 5 تعرف أن عشرتين و 3 عشرات تساوي 5 عشرات. في العلبة 10 قطع، لذلك تستطيع أن ترى أن 20 قطعة + 30 قطعة = 50 قطعة. مثال آخر :
| |
|
| 4 | | 4 | عشرات | | 40 | | 2 | | 2 | عشرتان | | 20 | | 6 | | 6 | عشرات | | 60 | |
تستطيع أن تعرف أن 4 + 2 = 6 ، 4 عشرات + عشرتين = 6 عشرات، و 40 + 20 = 60. العدد 6 في الـ 60 تُعدُّ ست عشرات، لأنها تقع في خانة العشرات. أنت تجمع فيها الآحاد. لكن يجب أن تكتب المجموع في خانة العشرات. ويجب أن تتذكر كتابة صفر في خانة الآحاد، لتظهر أن المجموع يكون عشرات، وليس آحادًا.
هنا مثال ثالث :
| |
|
| 8 | | 8 | عشرات | | 80 | | 9 | | 9 | عشرات | | 90 | | 17 | | 17 | عشرة | | 170 | |
مجموع العشرات هنا يكون سبع عشرة عشرة. سبع عشرة عشرة تكون مثل عشر عشرات وسبع عشرات. لكن عشر عشرات تساوي 100. لذلك يجب عليك كتابة المجموع في خانتي العشرات والمئات، وتكتب صفرًا في منزلة الآحاد لتظهر أن الجواب يكون مائة واحدة، وسبع عشرات وبدون آحاد.
جمع العشرات والآحاد:
هَبْ أنه يوجد 23 ولدًا و24 بنتًا في مسرحية مدرسية. لإيجاد العدد الإجمالي للأطفال، يجب عليك أن تجمع 23 و 24.
| |
|
| عشرتان | و | 3 | آحاد | | 23 | | عشرتان | و | 4 | آحاد | | 24 | | 4 عشرات | و | 7 | آحاد | | | |
يُعدُّ العددان 23، 24 من الأعداد ذات الخانتين. عندما تجمع أعدادًا ذات خانتين، فإنك تجمع الآحاد أولاً. في هذا المثال، ثلاثة آحاد وأربعة آحاد تكون 3 + 4 = 7. أنت تكتب مجموع الآحاد في خانة الآحاد من الجواب.
بعد ذلك اجمع العشرات. عشرتان وعشرتان تصبح 2 + 2 = 4. تحل الـ 4 محل أربع عشرات. تكتب مجموع العشرات في خانة العشرات من الجواب.
لذلك يكون هناك 47 طفلاً في المسرحية المدرسية. هنا مثال آخر :
أولاً تجمع الآحاد: 2 + 3 = 5. بعد ذلك تجد أن سبع عشرات وأربع عشرات: تساوي إحدى عشرة عشرة. إحدى عشرة عشرة تكون مثل عشر عشرات وعشرة واحدة، أو مائة واحدة وعشرة واحدة. لذلك يجب عليك أن تكتب مجموع العشرات في خانتي العشرات والمئات من الجواب. عندما توجد عدة مضافات، فغالباً ما نتكلم عن الآحاد، العشرات والمئات كأعمدة. عندما تجمع أعمدة، يجب عليك تعلم التفكير في الجمع. من المفيد الاحتفاظ بنوع من السجل في البداية.
وبالممارسة، يُصبح من السهل جمع أعداد ذات خانتين وأعمدة طويلة.
كيف تنقل (تحمل):
عندما تجمع أعدادًا ذات خانتين كثيراً ما يكون مجموع عمود الآحاد عشرة أو أكثر. لجمع مثل هذه الأعداد، يجب عليك تعلم الحمل.
بإمكانك أن تجمع أعمدة أطول من أعداد ذات خانتين بالطريقة نفسها.
أولاً، اجمع عمود الآحاد : 4 + 2 = 6 و 6 + 7 = 13. ثلاث عشرة هي عشرة واحدة وثلاثة آحاد. اكتب الـ 3 في خانة الآحاد من الجواب. انقل العشرة الواحدة إلى عمود العشرات بكتابة 1 في أعلى عمود العشرات.
الآن اجمع عمود العشرات : 1 + 2 = 3، 3 + 5 = 8 و 8 + 1 = 9. هذه الـ 9 تعني تسع عشرات. اكتب الـ 9 في خانة العشرات
جمع أعداد ذات ثلاث خانات وأربع خانات ليس بأكثر صعوبة من الأمثلة السابقة. يجب أن تتذكر دائماً أن عليك المحافظة على الأعمدة مستقيمة وأن تجمع الآحاد، ثم العشرات ثم، المئات، وهكذا، بالترتيب. إليك المثال التالي:
أولاً : اجمع عمود الآحاد : 1 + 3 + 9 = 13. اكتب الثلاثة في خانة الآحاد من الجواب. انقل العشرة بكتابة 1 عن العشرة الواحدة في أعلى عمود العشرات.
بعد ذلك، اجمع عمود العشرات:1 + 7 + 0+ 3 = 11. هذا ليس أحد عشر من الآحاد. إنه إحدى عشرة عشرة. إحدى عشرة عشرة تكون مائة واحدة وعشرة واحدة. لذلك اكتب 1 عن العشرة الواحدة في خانة العشرات من الجواب. وانقل المائة بكتابة 1 عن المائة الواحدة في أعلى عمود المئات.
الآن اجمع عمود المئات : 1 + 3 + 4+ 1 = 9. هذه الـ 9 تكون مئات. اكتب 9 في منزلة المئات من الجواب.
فيكون المجموع 913. بإمكانك استعمال أسلوب النقل نفسه مع الآلاف والأعداد الأكبر. إليك مثالاً يكون فيه العدد الذي تحمله أكثر من عشرة واحدة.
أولاً، اجمع عمود الآحاد : 7 + 9 + 8 = 24. أربعة وعشرون تساوي عشرتين وأربعة آحاد. اكتب الـ 4 في خانة الآحاد من الجواب. احمل العشرتين إلى عمود العشرات بكتابة 2 في أعلى عمود العشرات.
الآن، اجمع عمود العشرات : 2 + 3 + 2 + 1 = 8. هذه الـ 8 تعني ثماني عشرات. اكتب 8 في خانة العشرات من الجواب.
فيكون المجموع 84. الأعداد التي تحملها في كثير من الأحوال تكون عشرينات أو ثلاثينات أو أربعينات وهكذا.
التحقق من الجمع
يقوم الأشخاص الحريصون دائماً باختبار جمعهم للتحقق من صحة الجواب. توجد عدة طرق للتحقق من ذلك.
الجمع إلى أعلى:
لقد تعلمت جمع عمود من الأرقام بأن تبدأ من الأعلى وتجمع إلى الأسفل. بعد أن تكتب المجموع تستطيع التحقق من جوابك عن طريق
الجمع إلى أعلى ـ أي الابتداء من أسفل العمود والجمع إلى أعلى باتجاه القمة. إليك هذا المثال :
إذا حصلت على الجواب نفسه عندما تجمع إلى أعلى كالذي حصلت عليه في الجمع إلى أسفل، فعلى الأرجح، يكون جوابك صحيحًا.
الطرح:
يمكن أن يُستعمل للتحقق من مسائل بمضافين فقط. ★ تَصَفح:
الطرح.
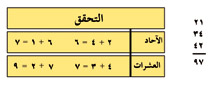
للتحقق من الجمع، اطرح واحدًا من المضافين من المجموع، مثلاً، اطرح 736 من 1158. يجب أن يكون حاصل الطرح مساويًا 422 إذا كان الجمع صحيحاً.
التقدير أو التخمين:
طريقة جيدة للتحقق من الجمع لكنها لا تستطيع اكتشاف الأخطاء الصغيرة. إذا استخدمت التقدير قبل حل المسألة سيكون لديك فكرة عن الجواب مُقدماً. يجب عليك التعود دائماً على تقدير جوابك أولاً، إليك هذا المثال :
توجد أساليب أخرى للتحقق مستعملة في الحساب، بعضها يمكن أن يُستعمل للجمع.
قواعد الجمع الواجب تذكرها
1- تذكَّر ماذا يعني الجمع. تستطيع أن تعرف الإجابات لمسائل الجمع بوساطة العدّ. لكن من الأسرع والأسهل أن تفكر في الإجابات.
2- تعلَّم حقائق الجمع الـ 81 سيساعدك على التفكير في إجابات مسائل الجمع.
3- تستطيع أن تضع المضافات في أي ترتيب دون تغيير المجموع في المعادلة. مثلاً 3+2+7 = 12، 2+7+3 = 12 و7+3+2 = 12.
4- تستطيع أن تجمع فقط الكميات ذات النوع نفسه ـ أي يجب أن تجمع آحادًا إلى آحاد وعشرات إلى عشرات، ولكن احذر من خلطها معًا.
التسلية بالجمع
 |
لغز الأرقام |
لغز الأرقام:
يرسم كل لاعب على ورقة فارغة خطوطاً رأسية وعرضية.
ثم يحاول كل واحد ملء الفراغات بالأعداد من 1 إلى 9 بحيث إذا جُمعت ثلاثة أعداد أفقياً أو رأسياً أو قطرياً يكون المجموع 15. يجب على اللاعب أن يستعمل كل عدد من 1 حتى 9. اللاعب الذي يحصل على الجواب الصحيح أولاً هو الذي يربح.
 |
الغمزتان |
الغمزتان:
جَهِّز رزمة من 20 بطاقة، واكتب عليها الأعداد من 1 إلى 10، بحيث تكون لكل عدد بطاقتان. اقسم رزمة البطاقات إلى كومتين، وضَعْ وجه كل كومة
للأسفل أمام كل واحد من اللاعبين. يقلب اللاعب الأول بطاقة ويعرضها حتى يراها هو واللاعب الآخر، ويفعل اللاعب الآخر الشيء نفسه من الكومة الثانية. اللاعب الذي يرى أولاً أن مجموع الأرقام على البطاقتين عشرة أو أكثر ينادي غمزتين! ثم يأخذ البطاقتين. إذا كان مجموع البطاقتين لايساوي عشرة أو أكثر يقوم اللاعبان بإعادتهما مرة أخرى إلى الكومتين. عندما يتم قلب جميع البطاقات بهذه الطريقة، فإن اللاعب الذي معه معظم البطاقات هو الذي يربح.
أمثلة للتدريب على الجمع
في كل من المسائل الست الأولى، ما العدد الذي يجب أن يستعمل ليحل محل ن؟
| |
|
| 1) | 5+2=7 | | 4) | 3 + 6 = ن | | 2+ن=7 | | | 6+3=ن | | | | | | | 2) | 8+6=14 | | 5) | 7+9=ن | | ن+8= 14 | | | 9+ن=16 | | | | | | | 3) | 5+9=14 | | 6) | 8+ن=13 | | 9+5=ن | | | 5+8=ن | |
| |
|
| 7) | 4 | | 9) | 24 | | 11) | 5 | | 13) | 35 | | 2 | | | 2 | | | 6 | | | 6 | | | | | | | | | | | | | 8) | 14 | | 10) | 34 | | 12) | 25 | | 14) | 45 | | 2 | | | 2 | | | 6 | | | 6 | | | | | | | | | | | | |
| |
|
| 15) | 40 | | 16) | 20 | | 17) | 60 | | 18) | 50 | | 30 | | | 80 | | | 70 | | | 90 | | | | | | | | | | | | | 19) | 10 | | 20) | 37 | | 21) | 56 | | 22) | 74 | | 70 | | | 42 | | | 33 | | | 65 | | | | | | | | | | | | | 23) | 65 | | 24) | 43 | | 25) | 14 | | 26) | 65 | | 23 | | | 52 | | | 64 | | | 18 | | | | | | | | | | | | | 27) | 29 | | 28) | 37 | | 29) | 98 | | 30) | 75 | | 48 | | | 56 | | | 69 | | | 58 | | | | | | | | | | | | | 31) | 3 | | 32) | 6 | | 33) | 6 | | 34) | 7 | | 9 | | | 8 | | | 5 | | | 8 | | 4 | | | 6 | | | 4 | | | 4 | | 6 | | | 3 | | | 7 | | | 6 | | | | | | | | | | | | |
| |
|
| 35) | 249 | | 36) | 765 | | 37) | 395 | | 129 | | | 182 | | | 489 | | | | | | | | | | 38) | 525 | | 39) | 618 | | 40) | 311 | | 482 | | | 489 | | | 299 | | | | | | | | | |
إجابات أمثلة التدريب
| |
|
| 1) | 5 | 16) | 100 | 31) | 22 | | 2) | 6 | 17) | 130 | 32) | 23 | | 3) | 14 | 18) | 140 | 33) | 22 | | 4) | 9 ، 9 | 19) | 80 | 34) | 25 | | 5) | 16 ، 7 | 20) | 79 | 35) | 378 | | 6) | 5 ، 13 | 21) | 89 | 36) | 947 | | 7) | 6 | 22) | 139 | 37) | 884 | | 8) | 16 | 23) | 88 | 38) | 1,007 | | 9) | 26 | 24) | 95 | 39) | 1,107 | | 10) | 36 | 25) | 78 | 40) | 610 | | 11) | 11 | 26) | 83 | 41) | 220 | | 12) | 31 | 27) | 77 | 42) | 150 | | 13) | 41 | 28) | 93 | 43) | 1,366 | | 14) | 51 | 29) | 167 | 44) | 2,850 | | 15) | 70 | 30) | 6133 | 45) | 9,919 | |
مقالات ذات صلة
المصدر: الموسوعة العربية العالمية