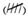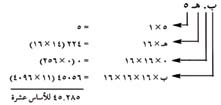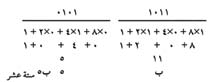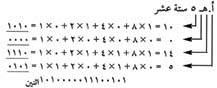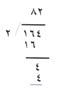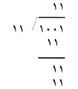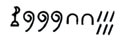أنظمـة الأعداد طرق للعد وتسمية الأعداد وتسمى أيضًا أنظمة الأرقام. ولأن الأعداد أفكار ذهنية، فإننا لانستطيع رؤيتها أو لمسها، لكن بإمكاننا استخدام رموز لتمثيلها. هذه الرموز نسميها أعدادًا. وتشمل الرموز التالية
ولنظامنا العددي عشرة أعداد أساسية فقط، تسمى
أرقامًا هي: 0، 1، 2، 3، 4، 5، 6، 7، 8، 9. وباستخدام هذه الرموز يمكن كتابة أي عدد. ويسمى هذا النظام بالنظام
العشري لأن أساسه العدد 10. وكلمة العشري مأخوذة من كلمة
عشرة، وبالتالي تعد عشرة
أساس أو
مقياس النظام العشري.
أنواع أنظمة الأعداد
بالإمكان استخدام عدد كلي أكبر من الواحد كأساس لبناء نظام للعد حيث يعتبر دوما عدد الأرقام المستخدمة أساسًا للنظام. ومن أمثلة ذلك: 1- النظام العشري أو ذو الأساس 10 ويستخدم 10 خانات 2- النظام الثنائي أو ذو الأساس 2 ويستخدم خانتين. 3- النظام الستة عشري أو ذو الأساس 16 ويستخدم 16 خانة.
النظام العشري:
يمثل هذا النظام الأعداد من خلال مجموعات يتكون كل منها من عشرة. ولنفترض أنك تود إحصاء الهللات أو القروش التي جمعتها. فبدلاً من عدها واحدة واحدة، يمكن عدها باستخدم مجموعات من 10، أي تضعها في ربط من 10، ومن ثم يكون ترتيب الربط في مجموعات بحيث توضع 10 منها في كل مجموعة كما هو موضح في الرسم.
كم هللة لدينا ؟ يمكن أن نجيـب على النحـو التالي: لدينـا مجموعتان في كل واحدة منها 10 ربط، وفي كل ربطة 10 هللات = 2× (10 × 10) = 200 ؛ و 4 ربط في كل منها 10 = 4 × 10 = 40، إضافة إلى 8 هللات منفـردة. أي لديـنــا ما مجموعــه 200 + 40 + 8 = 248 هللة.
 | نمودج توضيحي لانظام العشري | |
ولو عددنا الهللات أو القروش واحدة واحدة لحصلنا على نفس المجموع. وفي العد العشري نستخدم عددًا ذا خانة واحدة لنعد من 1 إلى 9 وفي العدد ذي الخانتين، يمثل الرقم الأيسر عدد المجموعات المكون كل منها من 10 بينما يمثل الرقم الأيمن العدد المنفرد. فمثلاً العدد 14 يمثل مجموعة واحدة من عشرة زائدًا 4 وحدات منفردة. وبعد 99 نستخدم أعدادًا ذات ثلاث خانات يمثل الأول منها من ناحية اليسار عدد
المئات (مجموعات من عشر عشرات). وبالتالي فالعدد 248 يمثل مائتين + 4 عشرات + 8 كما في الرسم أعلاه.
وتعتمد قيمة كل رقم في عدد عشري على خانتها (موقعها) في العدد. فمثلا يتكون العددان 482، 248 من نفس الأرقام لكنهما يمثلان عددين مختلفين لاختلاف خانات الأرقام في كل منهما.
ولكل خانة اسم يحدد قيمتها بالنسبة إلى 10. ففي العدد 248، تقع 8 في خانة الآحاد، 4 في خانة العشرات، 2 في خانة المئات. وفي الأعداد التي تزيد على ثلاثة أرقام، يطلق على الخانات الإضافية اسم خانة الألوف، ثم خانة عشرات الألوف، فلكل خانة قيمة تساوي 10 أضعاف قيمة الخانة التي على يمينها .
وهناك طريقة أخرى لإيجاد قيمة الخانة عن طريق استخدام (قوى العشرة) (أي 10 مضروبة في نفسها عددا من المرات. ويوضح الجدول التالي معنى قوى العشرة.
| الخانة | قوة العشرة | المــعـــنى | الرمز | | الآحاد | 0 | 1 | 010 | | العشرات | الأولى | 1×10 | 110 | | المئات | الثانية | 10×10 | 210 | | الألوف | الثالثة | 10×10×10 | 310 | | عشرات الألوف | الثالثة | 10×10×10×10 | 410 |
|
ويطلق مسمى الأس على كل من 2 في 210، 3 في 310، 4 في 410. وتسمى العشرة الأساس. ويدل الأس على عدد المرات التي يكون فيها الأساس معاملا، فمثلا 210 تعني استخدام العشرة مرتين كمعامل، أو 10×10. وبإمكاننا كتابة العدد 248 على النحو 200+40+ 8 أو على النحو (2×210) + (4×110) + 8.
إن قيمة أي عدد تساوي مجموع قيم الأرقام المكونة له. فالعدد 4206 يعني ¸4 آلاف زائدا مائتين زائدا لاعشرات زائدًا 6 آحاد·، أو (4×310) + (2+ 210) + (0×110) + (6×010) .
ويمكن أن نكتب أيضا 4206 على النحو (4×310) + (2 × 210) + (0×11) + (6 ×010). ويعني الأس (0) أن 10 ليست معاملا. لذا 6 × 010 تعبير آخر لـ 6 × 1.
النظام الثنائي:
الأعداد في مجموعات من اثنين وقوى الاثنين. وكلمة (ثنائي) مشتقة من لفظة (اثنين في كل مرة). ويستخدم هذا النظام رقمين فقط هما 0، 1، ويرمز العدد 10اثنين (صفر، واحد، أساس اثنين) (للعدد 2) الذي هو أساس النظام. ويعني 1 اثنين زائدا لا آحاد.
التجميع اثنين اثنين. توضح مجموعات المربعات التالية معنى عدة أنظمة عد ثنائية:
وفي العد الثنائي يستخدم رقم واحد للإشارة إلى لاشيء، وكذلك رقم واحد للإشارة إلى (واحد). وتستخدم أعداد ذات رقمين لكتابة 10 اثنين و 11 اثنين (2، 3 في النظام العشري). أما العدد الذي يليه 100 اثنين (4 في النظام العشري) فلابد له من ثلاثة أرقام. أما بعد 111 اثنين (7 في النظام العشري) فتستخدم أعداد ذات أربعة أرقام حتى تصل إلى 1111 اثنين (15 في النظام العشري) وهكذا.
إيجاد قيمة الخانة في الأساس 2 في الأعداد الثنائية لكل خانة قيمة تساوي ضعف قيمة الخانة التي على يمينها. فمثلا الـفراغ الذي في أقصى يمين العدد 1010 اثنين يعني 0 × 1 ويعني 1 الذي على يسار 0، 1 × 2، أما الذي يليه فيعني ( 2 × 2 بينمـا الذي في أقصـى اليسـار يعـني 1 × 2 × 2 × 2).
ويمكن التعبير عن قيمة خانة كل موقع بدلالة قوى 2. ويبين الجدول التالي معنى عدد قوى لـ 2.
وفي العدد 1010 اثنين، يعد الصفر في اليمين في خانة الآحاد، الواحد المجاور له في خانة 12، والصفر الذي إلى يســاره في منـزلة 22، والواحـد الذي في أقصى اليسار في خانة 32.
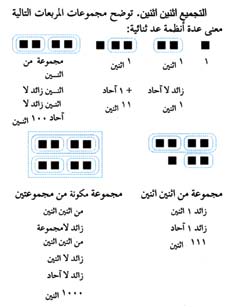
ويمكن تحويل الأعداد الثنائية إلى أعداد عشرية عن طريق إضافة رقـم منازل الأرقام بدلالة الأعداد العشرية. وتوضح الحسابات التاليــة كيفيــة تغيير العـــدد الثنائي 1011 إلى العدد العشري 13:
النظام الستة عشري:
هو مجموعات تحسب على أساس 16 وقوى 16. ويستخدم عادة النظام الستة عشري في صياغة الأوامر التي يقرأها الحاسوب من خلال نظام من الكلمات والرموز المسماة (لغة التجميع). ومن السهل تغيير الأعداد في النظام الستة عشري إلى النظام الثنائي، وهي اللغة التي يستخدمها الحاسوب فعلا.
أما الأرقام الستة عشر المستخدمة في النظام الستة عشري فهي 0، 1، 2، 4، 5، 6، 7، 8، 9، أ، ب، جـ، د، هـ، و حيث تمثل الأرقام الستة الأخيرة 10، 11، 12، 13، 14، 15.
أما الأساس 16 نفسه فيكتب 10 ستة عشر (واحد، صفر، أساس ستة عشر) والتي تعني ¸1 ستة عشر زائدا لا آحاد·.
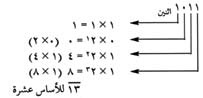
التجميع بالستة عشر توضِّح المجموعات التالية من النقاط معنى بعض الأعداد الستة عشرية ذات الرقمين.
إيجاد قيمة الخانة في الأساس 16. وكما في الأعداد العشرية أو الثنائية، فكذلك في الأعداد الستة عشرية يقع العدد الأيمن في خانة الآحاد بينما لكل خانة أخرى قيمة تساوي ضعف قيمة الخانة التي على يمينها. فمثلا في العدد 7 أ 5 ستة عشر، 7 تعني 7× 1، أ تعني أ × 16، 5 تعني 5 × 16 × 16.
ويبين الجدول التالي قيمة خانة عدد كل موقع بدلالة قوى 16.
ولتحويل الأعداد الستة عشرية إلى أعداد عشرية أضف في منازل الأرقام بدلالة الأعداد العشرية. وتوضح الحسابات أدناه كيفية تحويل العدد الستة عشر ب0 هـ 5 إلى العدد العشري 285,45.
تحويل الأعداد الثنائية إلى أعداد ستة عشرية. تستخدم الأعداد العشرة أرقامًا عديدة لتمثيل نفس العدد الذي يستخدم أرقامًا قليلة بالنسب لأساس أكبر.
ويمكن تحويل الأعداد الثنائية إلى أعداد ستة عشرية باتباع ثلاث خطوات: (1) ابتداءً من اليمين، ضع خطا تحت كل مجموعة مكونة من أربعة أرقام ؛ (2) حول كل عدد ثنائي من أربعة أرقام إلى عدد عشري ؛ (3) استبدل بالأرقام الستة عشرية المناسبة (أ إلى و) الأعداد العشرية التي تزيد على تسعة. وتوضح الحسابات التالية كيفية تحويل العدد الثنائي 10110101 إلى العدد الستة عشري ب 5:
ويمكن تحويل عدد ستة عشري مثل أ هـ 0 5 إلى العدد الثنائي 1010000011100101 بعكس الخطوات الثلاث السابقة، وكما هو مبين كالآتي:
استخدام أنظمة الأعداد
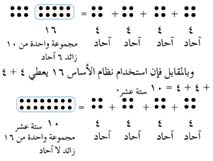
لنفترض أنه طلب منا حل مسألة الجمع: 4 + 4 + 4 + 4= ؟. لو استخدمنا النظام ذا الأساس 10، لكان الجواب 16،كما يتضح من المجموعات التالية من النقاط.
وبالمقابل فإن استخدام نظام الأساس 16 يعطي 4 + 4 + 4 + 4 = 10 ستة عشر.
تختلف الأعداد في كل من الإجابتين، ولكن عدد النقاط لا يتغير. وتتكون الأعداد طبقاً لمبدئي التجميع وقيم الخانات، وكذلك الحال مع الطرح والضرب والقسمة، والتي يمكن دراستها عن طريق حل مسائل باستخدام أنظمة أعداد متعددة للترقيم، وبالتالي اكتساب فهم أعمق لاستخدامات الأعداد في الحساب.
الحساب العشري:
يطلق مسمى الحقائق الحسابية على جمل مثل 4 + 5 = 9، 9 - 4 = 5، 9 × 5 = 45، 45 - 9 = 5. وتستخدم كثير من هذه الحقائق في الجمع والطرح والضرب والقسمة.
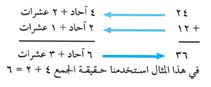
الجمع العشري هو طريقة لضم مجموعتين أو أكثر من مجمــوعة واحــدة فقط. ونستخدم مبدأ قيمة الخانة لجمع الآحاد مع الآحاد، والعشرات، وهكذا، كما يتضح من المثال التالي:
في هذا المثال استخدمنا حقيقة الجمع 4 + 2 = 6 وحقيقة 2 + 1 = 3 (يعني 2 من العشرات + 1عشرة = 3عشرات أو30). إذا فالمجموع هو 3 عشرات زائدًا 6 أو هو 36. وفي بعض المسائل، يكون المجموع في خانة أو أكثر مساويًا لعشرة أو أكثر، وعندها يجب
إعادة تجميع المجموعة، وهذا ما يسمى في الجمع بعملية
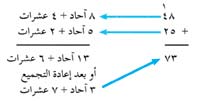
الحمل. وتبين المسألة التالية كيفية إعداد التجميع في الجمع العشري.
في هذه المسألة، تجمع الآحاد إلى 13، والتي يمكن إعادة تجميعها إلى 1 عشرة واحدة زائد 3 آحاد. ومن ثم نكتب 3 في خانة الآحاد و 1 ذا حجم صغير في خانة العشرات فوق الــ 4، ثم نجمع العشرات : 1 + 4 + 2 = 7 عشرات أو 70. ويكون المجموع هو 70 + 3 أو 73.
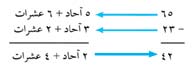
الطرح العشري. هو طريقة معاكسة للجمع، وتتبع مبادىء الجمع العشري نفسها.
في هذا المثال، استخدمنا الحقيقة 5 - 3 = 2، والحقيقة 6 - 2 = 4 (تعني 6 عشرات - 2 عشرات = 4 عشرات). ولطرح عدد كبير من عدد أصغر في أية خانة، يجب أن نعيد التجميع ويطلق أحيانًا على إعادة التجميع في الطرح مسمى
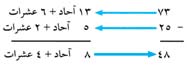
الاستلاف. ويوضح المثال التالي كيفية إعادة التجميع في الطرح العشري.
في خانة الآحاد يجب طرح 5 من 3، وهو الأصغر، لذا يعاد تجميع 7 عشرات زائد 3 لتصبح 6 عشرات زائدا 13 من الآحاد ونوضح ذلك بكتابة 1 ذي حجم صغير مقابل الـ 3. وشطب الـ 7 وكتابة 6 ذات حجم صغير أعلاها. استخدم حقيقة الطرح 13 - 5 = 8 لتطرح الآحاد، والحقيقة 6 - 2 = 4 لطرح العشرات.
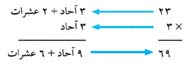
الضرب العشري هو طريقة لضم المجموعات المتساوية إلى بعضها البعض. وتعني حقيقة الضرب 4 × 6 = 24 أن 4 مجموعات ذات ستة أشياء تضم مامجموعه 24 شيئا. وإليك طريقة استخدام قيمة الخانة لضرب 23 في 3:
ابتداءًًا احسب: 3 × 3 آحاد = 9 آحاد، 3 × 2 عشرات = 6 عشرات، أو 60. ثم اجمع 60 + 9 = 69.
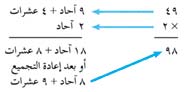
في الضرب نعيد التجميع عندما يكون حاصل الضرب في أية خانة مساويًا 10 أو أكثر.
في هذه المسألة، حاصل ضرب 2 × 9 هو 18، والذي يمكن إعادة تجميعه إلى 1 عشرة واحدة زائدًا 8 آحاد، ولذا نكتب 8 في خانة الآحاد ونكتب 1 ذا حجم صغير في خانة العشرات فوق الـ 4، ثم نضرب 2 × 4 = 8 في خانة العشرات ثم نضيف الـ 1 لنحصل على 9.
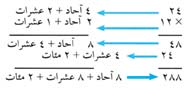
وعندما يكون للمضروب فيه أكثر من رقم واحد، نكرر العملية لكل رقم ثم نضيف حاصل الضرب:
اضرب أولا 24 في 2 مع كتابة 8 في خانة الآحاد، 4 في خانة العشرات، ثم اضرب 24 في 1 عشرة واكتب 4 في خانة العشرات، 2 في خانة المئات. ثم أضف النواتج لتحصل على 288.
القسمة العشرية. هي طريقة معاكسة للضرب. وتعمل على تجزئة مجموعة واحدة إلى عدة مجموعات من نفس الحجم. وفيما يلي طريقة قسمة 69 على 3:
احسب أولا : ¸6 عشرات - 3 = 2 عشرات·. اكتب 2 في خانة العشرات فوق الـ 6. ثم احسب: 9 آحاد - 3 = 3 آحاد. اكتب 3 في خانة الآحاد فوق الـ 9. إذا 69 - 3 = 2 عشرات + 3 آحاد أو 23.
وكذلك يجعل مبدأ قيمة الخانة من قسمة الأعداد الكبيرة أمراً سهلاً.
احسب أولاً: ¸16 عشرة - 2 = 8 عشرات·. اكتب 8 في خانة العشرات فوق الـ 6. ثم احسب 4 آحاد - 2 = 2 آحاد. اكتب في خانة الآحاد فوق الـ 4. إذا 164 - 2 = 8 عشرات + 2 آحاد أو 82.
الحساب الثنائي:
له عدد محدود من الحقائق لأنه يستخدم رقمين فقط هما 0 و 1.
الجمع الثنائي يعتمد على الحقائق التالية فقط:
0 + 0 = 0 ، 0 + 1 = 1 ، 1 + 0 = 1، 1 + 1 = 10
وفيما يلي طريقة استخدام هذه الحقائق لجمع 11 + 11:
أولاً نستخدم حقيقة الجمع 1 + 1 = 10 (يعني 1 اثنين) لجميع الآحاد. أعد تجميع 10 اثنين إلى 1 اثنين زائدًا لا آحاد. اكتب0 في خانة الآحاد و 1 ذا حجم صغير فوق عمود الاثنينات : ثم اجمع الاثنينات: 1 + 1 = 10 ؛ 10 + 1 = 11. اكتب 1 في خانة الاثنينات، 1 في خانة الأربعات. وبالتالي : 11 اثنين + 11 اثنين = 110 اثنين.
الطرح الثنائي. وأساسه أربع حقائق.
0 - 0 = 0، 1 - 0 = 1 ، 1 - 1 = 0 ، 10 - 1 = 1
وباستخدام هذه الحقائق اطرح 11 من 110.
الطرح الثنائي. المعنى (بعد إعادة التجميع مرتين) الطرح العشري.
في خانة الآحاد علينا طرح 1 من 0 لذا نعيد تجميع 1 أربعة زائد 1 اثنين زائد لا آحاد إلى 1 أربعة زائد لا اثنين زائد 10 آحاد، ثم نستخدم الحقيقة 10 - 1 = 1 لطرح الآحاد. ولطرح الاثنينات، علينا مرة أخرى طرح 1 من 0 لأن إعادة التجميع السابق ترك. في خانة الاثنينات. أعد تجميع 1 أربعة زائد لا اثنينات إلى لا أربعات زائد 10 اثنينات واستخدم الحقيقة 10 - 1 = 1.
الضرب الثنائي يستخدم الحقائق التالية:
0 × 0 = 0، 0 × 1 = 0 ، 1 × 0 = 0، 1 × 1 = 1
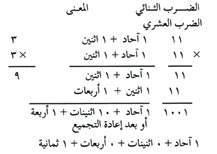
حاصل ضرب أي رقمين يساوي دائمًا 0 أو 1، لكن علينا إعادة التجميع عندما نضيف نتائج الضرب لإكمال أي مسألة ضرب. وكمثال إليك طريقة ضرب 11 × 11:
اضرب واكتب حاصل الضرب كما تفعل في النظام العشري، مستخدما حقائق الضرب الثنائي عند إضافة نتائج الضرب الجزئية. انزل الـ 1 في خانة الآحاد. أضف الاثنينات : 1 + 1 = 10. أعد تجميع 10 اثنينات إلى 1 أربعة زائد لا اثنينات. اكتب 0 في خانة الاثنينات وأضف 1 إلى 1 في خانة الأربعات: 1 + 1 = 10. اكتب 0 في خانة الأربعات و 1 في خانة الثمانيات لتحصل على 1001.
القسمة الثنائية معاكسة للضرب الثنائي. يوضح المثال التالي القسمة على عدد ثنائي ذي رقمين:
لقسمة 11 إلى 1001 احسب ¸11 أكبر من 10 لكن أصغر من 100 لذا يجب أن تمتد إلى 100 مرة واحدة·. اكتب 1 فوق الصفر الثاني، ثم اكمل الحل بالضرب ثم الطرح كما في مسائل الأعداد العشرية، لكن تذكر استخدام حقائق الطرح الثنائي .
الحساب الستة عشري:
له من الحقائق أكثر مما للحساب العشري لأنه أكثر أرقامًا (0إلى 9 زائدًا أ إلى و).
الجمع الستة عشري. بالإمكان استخدام الجدول التالي لمعرفة الحقائق الأساسية عن الجمع الستة عشري .
فمثلا لإيجاد مجموع 6 + أ، أوجد أولا الصف الذي يبدأ بـ 6، ثم حرك أصبعك باتجاه اليسار مرورا بهذا الصف حتى تصل إلى العمود الذي يبدأ في أعلاه بـ أ. سيكون إصبعك على الـ 10 (تعني 1 ستة عشر زائدًا لا آحاد) وهو مجموع 6 زائدًا أ.
استخدم الجدول لحل المسألة التالية:
استخدم أولا الحقيقة جـ + 1 = د لجمع الآحاد، ثم استخدم الحقيقة 2 + 8 = أ (2 ستة عشر + 8 ستة عشر = أ ستة عشر).
وعندما يكون المجموع في أية خانة أكبر من و، أعد التجميع بدلالة الأساس 16 كما هو مبين في المثال التالي.
وكما يتضح من المثال، فإن هـ + 4 = 12 في خانة الآحاد. وبإعادة تجميع 12 آحاد إلى 1 ستة عشر زائد 2 آحاد. اكتب 2 في خانة الآحاد و 1 ذا حجم صغير في خانة الستة عشر فوق الـ 6، ثم أضف الستة عشر: 6 + 3 = 9 ستة عشري، 9 ستة عشر زائد الـ 1 ستة عشري التي حصلنا عليها عن طريق إعادة التجميع يساوي أ ستة عشري.
الطرح الستة عشري بإمكاننا استخدام جدول حقائق الجمع الستة عشري لنوجد أيضًا حقائق الطرح الستة عشري. فمثلا لطرح د من 12، أوجد أولا العمود الذي يبدأ بـ د، ثم انزل بإصبعك على طول هذا العمود حتى تصل إلى 12، ثم حرك إصبعك يسارًا على طول هذا الصف حتى تصل إلى أول رقم لتجد الجواب 5.
لقد طرحنا الآحاد باستخدام الحقيقة 8 - 6 = 2 بينما في خانة الستة عشر استخدمنا هـ - ب = 3.
إذا كان الرقم المطروح أكبر من الرقم الذي يعلوه، فنحتاج إلي إعادة التجميع كما يتبين من المثال التالي:
الطرح الستة عشري المعنى الطرح العشري
بما أن جـ أكبر من 4 في خانة الآحاد، يتوجب علينا إعادة تجميع 3 ستة عشر زائد 4 آحاد إلى 2 ستة عشر زائد 14 آحاد. اشطب الـ 3، واكتب 2 ذات حجم صغير أعلاها، واكتب 1 ذا حجم صغير بجوار الـ 4، ثم استخدم حقيقة الطرح 14 - جـ = 8 لطرح الآحاد. وللطرح في خانة الستة عشر استخدم الحقيقة 2 - 1 = 1.
الضرب الستة العشري يستخدم أيضا حقائق أكثر من الضرب العشري. وبالإمكان استخدام الجدول التالي لإيجاد الحقائق الأساسية عن الضرب الستة عشري.
فمثلا لإيجاد حاصل الضرب 5 × 9، أوجد أولا الصف الذي يبدأ بـ 5، ثم حرك إصبعك يمينا، توقف عند العمود الذي يبدأ في أعلاه بـ 9. سيتوقف أصبعك عند د 2 (2 ستة عشر زائد د آحاد).
استخدم الجدول لحل المسألة التالية في الضرب الستة عشري، وتذكر إعادة التجميع إذا كان الناتج في أية خانة أكبر من و.
في خانة الآحاد استخدمنا الحقيقة 6 × 8 = 30، وأعدنا تجميع الـ 30 آحاد إلى 3 ستة عشر و 0 آحاد. اكتب0 في خانة الآحاد و 3 ذات حجم صغير في خانة الستة عشر فوق الـ 5. ثم اضرب 5 × 8 لتحصل على 28 وأضف الـ 3 لتحصل على ب 2 وحيث إن 5 كانت في خانة الستة عشر، فإن النتيجة النهائية تتكون من ب في خانة الستة عشر، و 2 في خانة الستة عشر مضروبة في الستة عشر.
وعندما يتكون المضروب فيه من أكثر من رقم، كرر العملية لكل رقم وأضف النواتج، كما هو موضح في المثال التالي:
اضرب أولا ب2 في 2 حيث ب × 2 = 16 آحاد. اكتب 6 في خانة الآحاد وأعد التجميع بإضافة 1 ذي حجم صغير في خانة الستة عشر، ثم اضرب 2 ستة عشر × 2 لتحصل على 4 ستة عشر وأضف الـ 1 للستة عشر التي أعيد تجميعها. اكتب 5 في خانة الستة عشر، ثم اضرب ب 2 في 5 (ستة عشر). ب× 5 = 37 من جدول الضرب الأساسي. اكتب 7 في خانة الستة عشر وأعد تجميع الـ 3 بكتابة 3 ذات حجم صغير فوق الـ 1 الذي حصلنا عليه من إعادة التجميع في الخطوة الأولى استخدم الحقيقة الأساسية 2 × 5 = أ، ثم أ + 3 = د واكتب د في خانة الستة عشر تربيع. وبجمع الآحاد ومجموعة الستة عشر، ومجموعة الستة عشر مضروبة في مجموع الستة عشر نحصل على 6 جـ د .
القسمة الستة عشرية يمكن أيضا استخدام جدول الضرب الستة عشري لإيجاد حقائق القسمة. فمثلا لقسمة ب على 58 أوجد أولا العمود الذي يبدأ بـ ب. انزل إصبعك على طول العمود حتى تصل إلى 58. وفي أقصى اليسار من هذا الصف ستجد الإجابة وهي 8.
استخدم الجدول لحل المسألة التالية:
احسب ¸د ستة عشر مقسومة على 8 تساوي 1 ستة عشر·. اكتب 1 فوق الـ د. اضرب 1 × 8 واكتب الناتج 8 تحت د. اطرح 8 من د باستخدام جدول الضرب الستة عشري. أكمل الحل كما لو كنت في القسمة العشرية، لكن باستخدام حقائق الحساب الستة عشري.
نبذة تاريخية
نشأة نظام الأعداد. كان للشعوب البدائية عدة طرق لتسجيل الأعداد القليلة التي يحتاجونها. كان بإمكان الراعي أن يجمع عددا من الحصى يمثل عدد الخراف في القطيع بحيث تمثل الحصاة الواحدة خروفا واحدًا. وكان الكيس من الحصى يعني كامل القطيع. وبمقارنة الحصى مع القطيع، يتمكن الراعي من معرفة إن كان أحد الخراف مفقودًا. ويطلق علماء الرياضيات على هذا النوع من المقارنة علاقة واحد إلى واحد.
وفيما بعد طور الناس طرقا أخرى لتسجيل أعداد الأشياء التي يمتلكونها، فقاموا بربط عقد في حبل جلدي أو قاموا بخدش علامة تسجيل على جانب صخرة، ومن ثم قاموا بمقارنة العقد أو العلامات مع كل شيء على حدة. ثم لجأ الناس إلى استخدام الكلمات للتعبير عن الأعداد، فبينت
الكم وساعدت الناس علي مقارنة الأشياء ذهنيا. فمثلا استخدم الناس كلمة
جناح للتعبير عن شيئين، وللتعبير عن أربعة أشياء استخدموا اسم فاكهة تنمو في عنقود من أربع ثمرات. واستخدموا كلمة يد للتعبير عن 5 أشياء. وقد ظهرت هذه العلاقة بين الأعداد والأسماء في لغات بدائية عديدة حيث أثبتت بداية تفكير الناس في الأعداد. لقد ميزوا فكرة
الثلاثية لمجموعة تحتوي على ثلاثة أشياء سواءً كانت هذه الأشياء سمكًا أو حصى أو علامات تسجيل.
وأخيرا، شرع الناس في العد عن طريق وضع الأسماء الممثلة للأرقام في ترتيب معين، فنطقوا أو كتبوا الكلمة التي تعني واحدًا ثم الكلمة التي تعني اثنين، ثم الكلمة التي تعني ثلاثة، وهكذا.
ومع مرور الوقت طوّرت الشعوب في أنحاء مختلفة من العالم أنواعًا عديدة من أنظمة العد، بعضها اعتمد على الخمسة كأساس، وبعضها على العشرة، بل إن بعضها اعتمد كأساس على الاثني عشر أو الستين. وما زلنا إلى يومنا هذا نستخدم بعض هذه القياسات المأخوذة من هذه الأنظمة مثل الـ 12 بوصة في القدم والـ 60 دقيقة في الساعة.
وفي معظم أنظمة الترقيم القديمة، كان الناس يصيغون الأعداد بمجرد تكرار الرموز الأساسية، وإضافة قيمها ليحصلوا على العدد المطلوب. وقد اتبع المصريون والإغريق والرومانيون أنظمة عد من هذا القبيل. أما العرب فقد اتبعوا نظاما للترقيم متفوقا على سائر الأنظمة الأخرى، وهذا النظام اعتمد علي مبدأ قيمة الخانة واستخدموا رمزا يعني لاشيء أو الصفر. وأصبح هذا النظام نظام العد العشري المتبع في معظم أنحاء العالم.
نظم الأعداد المصرية. في حوالي عام 3000 ق.م استخدم المصريون اللغة الهيروغليفية (كتابة الصور) لكتابة الأعداد، كما هو موضح فيما يلي.
واعتمد هذا النظام على أساس 10، لكنه لم يشتمل على رمز للصفر، كما أنه لم يستخدم مبدأ قيمة الخانة، وصاغ المصريون الأعداد بوضع الرموز الأساسية بجانب بعضها البعض. فمثلا، كتبوا العدد 326,1 على النحو التالي:
وطبقا لهذا النظام، كان بإمكان المصريين وضع الرموز في أي ترتيب كان لأن قيمة الرمز لاتعتمد على موقعه.
نظام الأعداد الإغريقية. في حوالي العام 500 ق.م، طور الإغريق نظامًا للعد يعتمد العشرة أساسًا، ويستخدم أحرف الهجاء الإغريقية السبعة والعشرين - 24 منها مستخدمة حاليًا إضافة إلى 3 أحرف لم تعد تستخدم - وكانت الأحرف التسعة الأولى ترمز إلى الأعداد من 1 إلى 9، وكانت الأحرف التسعة التالية ترمز للعشرات، من 10 إلى 90، وأما الأحرف التسعة الأخيرة فكانت ترمز إلى المئات من 100 إلى 900. وقام الإغريق بصياغة الأعداد عن طريق ربط هذه الرموز وإضافة قيمها.
نظام الأعداد الرومانية. اعتمد على الأحرف كرموز للأعداد، لكن النظام الروماني القديم في حوالي 500 ق.م اختلف عن النظام القائم اليوم. فمثلا،
كتب الرومان 4 على النحو iiii
، وكتبوا 9 على النحو viiii
، واستخدموا الرمز للعدد 50
| و للعدد 1000 استخدم الرمز | |
أما اليوم فنستخدم iv للعدد 4، ix للعدد 9، l للعدد 50 و m للعدد 1000. وتبين الأعداد lx,vi، xv مبدأ الإضافة. وعندما يرمز الأول من رمزين لعدد أكبر من الثاني، فإننا نضيف قيمة الأول إلى الثاني لنحصل على قيمة العدد المركب. وبالتالي فالعدد الروماني vi يمثل 6 أو 5 + 1 ؛ xv يمثل العدد 15 أي 10 + 5 ؛ lx يمثل العدد 50 + 10 = 60.
أما الأعداد iv وix فتوضح مبدأ الطرح، فعندما يرمز الأول من رمزين لعدد أصغر من الثاني، فإننا نطرح قيمة الأول من قيمة الثاني لنحصل على قيمة العدد المركب، وبالتالي في العدد الروماني iv نطرح 1 من 5 لنحصل على 04.
نظام الأعداد البابلية. يستخدم الرموز المسمارية (إسفينية الشكل)، وهو نظام قديم يعتمد على الـ 60، وعمل به حوالي العام 2100 ق.م. وفي هذا النظام، يحتوي العدد على مجموعة من الرموز إذ تمثل إحدى المجموعات عدد الآحاد وتمثل المجموعة التالية الستينات، وتمثل أخرى الأعداد (60 * 60)، وهكذا.
وبحلول العام 1500 ق.م، طور البابليون نظاما أساسه 10. وفي هذا النظام يكون الألف تشكيلا من رمزي العدد عشرة والعدد مائة.
نظام الأعداد الهندية العربية. استخدم علماء الرياضيات الهنود نظاما أساسه 10، وذلك في القرنين الرابع والثالث قبل الميلاد، وأوجد الهنود رمزا لكل عدد من الواحد إلى التسعة. وكان لكل أس للعدد 10 اسما، وقد استخدموا هذه الأسماء عند كتابة الأعداد، فمثلا كتب الهنود ¸1 ساتا، 3 داسان، 5· للعدد الذي يكتب 135.
ومن المحتمل أن الهنود اكتشفوا في القرن السابع قبل الميلاد طريقة للتخلص من مسميات الخانات، واخترعوا الرمز سونيا (يعني الخالي)، والذي نسميه (الصفر). وبهذا الرمز استطاعوا كتابة ¸105· بدلا من ¸1 ساتا، 5·.
وخلال القرن الثامن الميلادي، تعلم العرب الحساب من الكتابات العلمية للهنود والإغريق وطوروها، ثم في القرن الثامن ألفوا كثيرًا من الكتب في الرياضيات ترجمت إلى اللاتينية بعد مرور حوالي 300 عام. وقد أدخلت هذه الترجمات الأعداد الهندية العربية إلى أوروبا.
ومرت مئات السنين قبل أن يشيع استخدام النظام الهندي العربي. وقد حبذ الكثير من الناس الأعداد الهندية العربية لسهولة استخدامها في كتابة العمليات الحسابية، بينما فضل آخرون الأعداد الرومانية لتعودهم حل العمليات الحسابية، على آلة تسمى العداد دون الحاجة إلى كتابة العمليات الحسابية، وبعد تطور الطباعة الآلية في القرن الرابع عشر الميلادي، ألفت كتب عديدة في مجال الرياضيات، عالج معظمها العمليات الحسابية باستخدام الأعداد الهندية العربية، ومن ثم عملت هذه الكتب على الانتشار الواسع لاستخدام النظام.
ويعد علماء الرياضيات نظام الأعداد العربية أحد أهم الاكتشافات المهمة في العالم، وتكمن أهميته في مبدأ قيمة الخانة واستخدام الصفر. مما سهل في عملية تمثيل الأعداد وإجراء العمليات الرياضية التي ستكون متعسرة عند استخدام أي نظام آخر.
إعادة اكتشاف أنظمة الأعداد. في أواخر القرن السابع عشر الميلادي، طور عالم الرياضيات والفيلسوف الألماني غوتفريت فلهلم لايبنيز (1646-1716م) نظام العد الثنائي،ولكن علماء الرياضيات لم يقتنعوا بجدوى هذا النظام حتى أواخر الأربعينيات من القرن العشرين عندما طورت أجهزة الحاسوب التي تستخدم النظام الثنائي إلى يومنا هذا.
وخلال الخمسينيات والستينيات من هذا القرن، أدرك العديد من رجال التعليم أهمية تدريس أنظمة الأعداد، وبدأ الطلبة دراسة الأنظمة المختلفة كجزء مما سمي بـ الرياضيات الحديثة. وقد أدى قيام الطلبة بالعمليات الحسابية عن طريق الأنظمة غير المألوفة إلى إكسابهم فهما أعمق للنظام العشري الشائع وللحساب بصفة عامة. بيد أنه في السبعينيات أدرك رجال التعليم أن الطلبة يحتاجون أيضا إلى المران في حل مسائل الحساب اليومية ولتعلم المهارات الحسابية الأساسية.
مقالات ذات صلة
المصدر: الموسوعة العربية العالمية