الطرح ( Subtraction )

الاستلاف	في الطرح يعني تحويل 10 من المطروح منه إلى آحاد، أو تحويل 100 إلى عشرات، أو تحويل 1000 إلى مئات، وهكذا.
الباقي.	في 12 - 7 = 5، العدد 5 هو الباقي، والباقي هو جواب مسألة الطرح.
حقيقة الطـرح	عبـارة أسـاسيــة في الطــرح مثــلا: 16-9 = 7 و 4 - 3 = 1 هما اثنتان من حقائق الطرح.
الباقي.	في 12 - 7 = 5، العدد 5 هو الباقي. ويعني أن 12 و 7 قد تمت المقارنة بينهما.
المطروح.	في 12 - 7 = 5، العدد المستبعد (7) هو المطروح.
المطروح منه.	في 12 - 7 = 5، العدد 12 هو المطروح منه.
الناقص	في الطرح يعني انقص أو استبعد ، فمثلا 12 ناقص 7 يكون 5.

الطرح بوساطة العد:

هنا مجموعتان من الكعك المغطَّى بالشكولاته.

كم كعكة في المجموعة الأولى؟

عدّها، في المجموعة الأولى 6 كعكات.

أخذت مريم 3 كعكات من المجموعة الثانية. فكم كعكة بقيت في المجموعة الثانية؟ عُدّها.

بقي فيها 3 كعكات. إنك عددت لتجد كم يكون عدد الكعكات الباقية إذا أخذت 3 من 6. لقد اكتشفت أن أخذ 3 من 6 يجعل الباقي 3.

الطرح بوسـاطة التفـكير:

لـدى أحمـد 5 كرات زجاجية، يريد مقايضة اثنتين منها بقلم رصاص. كم كرة زجاجية ستبقى لدى أحمد؟

غط كرتين في الصورة. يجب أن تكون قادراً على تحديد عدد الكرات الباقية بمجرد النظر إلى الصورة بدون أن تَعُد، يجب أن تتعلم أن تفكر 2 من 5 يَبْقى 3. ستبيِّن لك هذه المقالة الحقائق التي تحتاج إلى معرفتها كي تَطْرح بوساطة التفكير. فالتفكير في الجواب طريقة للطرح أسرع من طريقة العد.

تستطيع أن تتعلم التفكير في الجواب لمسألة طرح مما سبق وعرفته عن الجمع.

فمثلاً: أنت تعرف أن 3 و 2 تكون 5، هذا يعني أنك إذا أخذت 2 من 5 فإنه يبقى لديك 3. تستطيع التمرُّن على أسلوب الطرح هذا بكتابة حقائق الجمع والطرح معاً في مجموعات رباعية:

3 و 4 تكون 7
4 من 7 يبقى 3

4 و 3 تكون 7
3 من 7 يبقى 4

أسئلة الطرح:

تدلُّك عملية الطرح على عدد الأشياء الباقية عندما تستبعد مجموعة من الأشياء من مجموعة أخرى، كما تُمكِّنك أيضا من المقارنة بين مجموعتين من الأشياء. افرض أن لدى مريم 5 بالونات ولدى سميرة 3 بالونات.

كي تقارن بين المجموعتين عليك أن تجد الفرق بينهما. تستطيع أن تجد الفرق باستخدام الطرح. فعندما تطرح 3 من 5 تكتشف أن الفرق بين المجموعتين يكون بالونتين.

تستطيع استعمال الطرح أيضا لتجَد عدد الأشياء الأخرى المطلوبة. يحتاج حسن إلى 12 كرة زجاجية ولديه 5 منها. فكم كُرة أخرى يحتاج؟

عندما تطرح 5 من 12 تكتشف أن حسنًا يحتاج إلى 7 كرات أخرى ليصبح لديه 12 كرة.

يستطيع أن يدلّك الطرح على:

1- كم عدد الأشياء الباقية؟ 2- ما الفرق؟ 3- كم عدد الأشياء الأخرى المطلوبة؟

كتابة الطرح:

من الأفضل أن تَكْتُب مسائل الطرح وإجاباتها، فهذا يُعطيك سجلاً لتفكيرك.

تستطيع أن تعمل سجلاًّ بوساطة الصور:

تُبيِّن الصورة أن أخذ 3 من 5 يُبقي على 2. تستطيع أن تكتب هذا بالأرقام والكلمات:

3 من 5 الباقي 2

لكن يجب أن تتعلم أن تكتب بالأرقام والإشارات:

5 - 3 = 2

الإشارة (ـ) تعني أن تَطْرح أو تَستبعد. لذلك فإن 5-3 تعني (أخْذ 3 من 5).

نسمي الإشارة (-) إشارة الناقص، ونقرأ 5 - 3 على النحو: (5 ناقص 3).

تعني الإشارة (=) أن المجموعات في إحدى جهتي الإشارة (=) تكون مساوية للمجموعات في الجهة الأخرى منها. وهنا توضيح لكيفية عملها.

وهناك طريقة أخرى لاستعمال الأعداد والإشارات:

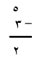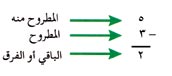
لكل جزء من مسألة الطرح اسم، فعندما نطرح لنعرف عدد الأشياء الباقية فإننا ندعو الجواب الباقي. وعندما نطرح لنقارن بين مجموعتين أو لنعرف عدد الأشياء الأخرى المطلوبة فإننا نُسمِّي الجواب الفرق. والعدد الذي يُؤخَذ منه المطروح يُسمي المطروح منه.

حقائق الطرح:

عند طرح مجموعة من مجموعة أخرى تكتشــف أن: 8 - 5 = 3، 6 - 3 = 3 و 12 - 5 = 7 ونُسمِّي تلك العبارات حقائق طرح.

كل حقيقة طرح تتكون من المطروح منه، والمطروح، والباقي أو الفرق. وتستطيع اكتشاف كل حقيقة من حقائق الطرح بنفسك بوساطة العد واستبعاد مجموعة أشياء من مجموعة أخرى. فمثلاً تستطيع التمرين عن طريق شطب المربعات كما فعلنا في مثال سابق.

بعض حقائق الطرح

هناك حقائق أخرى للطرح ؛ فمثلاً أي عدد ناقص نفسه يكون صفراً، لذلك 5-5=0 و 9-9 = 0، أيضاً أي عدد ناقص صفر يساوي العدد نفسه ، لذلك 6-0=6، و3 - 0= 3. من الأفضل أن تتعلم حقائق الطرح كي تستطيع استرجاعها دون أن تتوقَّف عندها والقيام بحسابها، لتكون قادرا على استعمالها لحل مسائل الطرح بطريقة صحيحة.

لكي تتعلم حقائق الطرح الأكثر صعوبة من المفيد أحياناً أن تعيد التجميع. فمثلاً كثير من الناس يجد أن طرح أعداد من عشرة يكون أسهل. افترض أنك تريد حل المسألة: 14-7=7 أنت تعرف أن 14 هي: عشرة واحدة وأربعة أحاد، لذلك باستطاعتك إعادة تجميعها على النحو التالي:

بإمكانك أولاً أن تستبعد 4. وبما أنك تعرف أن 7- 4=3 فإن عليك أن تستبعد أيضًا 3، لأن طرح 3 من 10 أمر سهل.

فأنت ترى أن 10 - 3 = 7. وعليه فإن: 14 - 7 = 07 وباستطاعتك اكتشاف طرق أخرى لتساعدك على تعلم حقائق الطرح.

طرح أعداد أكبر

ليس صعباً أن تطرح أعداداً أكبر إذا عرفت حقائق الطرح واستوعبت نظام الأعداد.

طرح العشرات والمئات:

افترض أن لديك 5 أكياس من الحلوى، وكل كيس يحتوي على 10 قطع من الحلوى. فيكون هذا بمثابة 50 قطعة من الحلوى. إذا وزعت منها 3 أكياس فكم قطعة من الحلوى بقيت لديك؟

المسألة هي: 5 أكياس - 3 أكياس أو 50 قطعة من الحلوى - 30 قطعة. تستطيع أن تجد الجواب عن طريق عَدِّ قطع الحلوى المتبقية لديك، وتستطيع أيضاً أن تجد الجواب باستعمال حقائق الطرح والتفكير.

فإذا عرفت أن 5 - 3 = 2 تستطيع أن ترى أن أخذ 3 أكياس من أصل 5 أكياس تُبقي على كيسين، وكل كيس يحتوي على 10 قطع من الحلوى، لذلك تستطيع أن ترى أن 50 - 30 = 20. حقيقة الطرح 5 - 3 = 2 ساعدت على إيجاد الجواب. وطرحك للعشرات يتم بنفس الطريقة التي تتبعها في طرح الآحاد، لكن يجب عليك أن تكتب الباقي في خانة العشرات، كما يجب عليك أن تضيف له صفراً لتبين أن الباقي عشرات وليس أحاداً.

طرح المئات يكون بنفس الطريقة:

افترض أن عليك طرح 3 أمتار من 5 أمتار حيث المتر يساوي 100 سم:

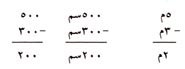تطرح المئات (والآلاف... إلخ) بنفس الطريقة التي استعملتها في طرح الآحاد والعشرات. مرة أخرى تستطيع أن ترى كيف أن معرفة حقائق الطرح تُساعدك على إيجاد الجواب.

طرح العشرات والآحاد:

لدى خالد 45 تذكرة سيقوم ببيعها. باع منها 23 تذكرة، فكم تذكرة تبقى لديه؟

أي كم 45 - 23؟ ندعو الأعداد مثل 45 و 23 أعداداً ذات خانتيْن ؛ لأن العدد 45 يتألف من خانتيْن هما 4 عشرات و5 آحاد، كما أن العدد 23 يتألف من خانتين، هما عشرون و 3 آحاد.

لتطرح عددًا واحدًا ذا خانتين من عدد آخر، عليك أن تبدأ بطرح الآحاد: 5 - 3 = 2 اكتب الاثنين في خانة الآحاد من الباقي:

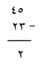ثم بعد ذلك اطرح العشرات: 4 - 2 = 2. تذكر أن:

4 - 2 تمثل العشرات وليس الآحاد، اكتب الاثنين في خانة العشرات من الباقي

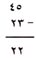وبالتالي يجب أن يبقى مع خالد 22 تذكرة.

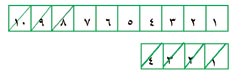
هنا مثال على طرح عددين من ثلاث خانات:

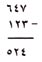أولاً: اطرح الآحاد: 7 - 3 = 4، اكتب الأربعة في خانة الآحاد من الباقي. بعد ذلك اطرح العشرات: 4 - 2 = 2، اكتب الاثنين في خانة العشرات من الباقي، ثم اطرح المئات: 6 - 1 = 5، اكتب الخمسة في خانة المئات. إن طرح أعداد ذات خانتين وثلاث خانات أمر سهل، لكن يجب عليك تَذَكّر أمريْن: إذ يجب أن تطرح الآحاد، العشرات، المئات، الآلاف...إلخ بنفس الترتيب. ابدأ دائماً من اليمين (من خانة الآحاد) وباشر العمل باتجاه اليسار. ثانياً: يجب أن تُدوِّن عملك بدقة بحيث يكون موقع العدد الباقي في الخانة المناظرة في كل خطوة.

كيفية الاستلاف:

عندما تطرح أعداداً أكبر فإنك لاتستطيع في كثير من الأحوال أن تحل المسألة مالم تعرف كيفية الاستلاف. فعلى سبيل المثال، ★ تَصَفح إلى المثال التالي: 62 - 27. كيف يمكنك أن تطرح 7 آحاد من اثنين من الآحاد؟ يساعد الاستلاف على حل مثل هذا النوع من الأمثلة.

لكي تستوعب الاستلاف عليك أن تتبع مثالاً معطى خطوةً خطوة. في المثال 62 - 27 الخطوة الأولى هي أن تَفْصل الأعداد إلى عشرات وآحاد:

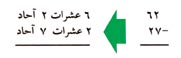لاتستطيع أن تطرح 7 آحاد من 2. لكن باستطاعتك أن تأخذ عشرة واحدة من المطروح منه وتحولها إلى آحاد، وتستطيع بذلك أن تحل المسألة.

لذا فإن 62 - 27 = 35. لاحظْ أن الآحاد في المطروح أكبر من الآحاد في المطرُوح منه مما تطلّب الاستلاف، أو تغيير عشرة من خانة العشرات، في المطروح منه، إلى الآحاد. هذا هو المقصود بالاستلاف. يمكنك، في حل المسائل، الاستلاف من المئات والألوف...إلخ.

يتعين عليك تدْوين المسألة في كل مرة تقوم فيها بالاستلاف، إذ يمكنك أن تفكر بالخطوات ثم كتابة أعداد بشكل مُصغر كدليل عليها. لنأخذ المثال السابق نفسه.

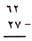قُمْ أولاً بدراسة المثال. ¸لا أستطيع أخذ 7 من 2· ثم فكر ¸لذلك يجب عليَّ تحويل عشرة إلى آحاد· ارسم خطَّاً خفيفاً على العدد 6 من المطروح منه واكتب 5 فوقه.

هذا يعني أنه يوجد الآن 5 عشرات فقط في خانة العشرات بدلاً من 6 عشرات. بعد ذلك اكتب واحداً بخط مُصَغَّر فوق العدد 2 مباشرة وإلى يساره، هذا يعني أنه يوجد الآن اثنا عشر من الآحاد بدلاً من اثنين:

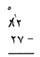تستطيع الآن أن تقوم بالطرح (7 آحاد من 12 من الآحاد يبقى 5). لقد فكَّرت، اكتب 5 في خانة الآحاد من الباقي. ¸عشرتان من 5 عشرات يبقى 3·. لقد فكَّرت، اكتب 3 في خانة العشرات من الباقي. وبهذا يكتمل المثال:

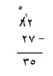نفس الأسلوب المتَّبع في استلاف عشرة يمكن استعماله في استلاف مئات وآلاف:

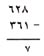أولا: اطرح واحدا من 8 آحاد واكتب 7 في خانة الآحاد من الباقي. لكنك ترى أنه لايمكنك أن تطرح 6 عشرات من عشرتين، إذ يجب عليك أن تستلف 100 أو 10 عشرات من الـ 600 من المطروح منه:

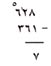ارسم خطّاً خفيفاً على الستة في المطروح منه واكتب 5 فوقها. فهذا يعني أنه يوجد الآن 5 مئات في خانة المئات بدلاً من 6.

بعد ذلك اكتب واحداً بخط مُصغَّر فوق العدد 2 مباشرة وإلى يساره. وهذا يعني أنه يوجد الآن 12 عشرة بدلاً من عشرتين. تستطيع الآن أن تنهي الطرح: 6عشرات من 12 عشرة يبقى 6. اكتب 6 في خانة العشرات من الباقي. 3 مئات من 5 مئات يبقى مائتان. اكتب 2 في خانة المئات من الباقي.

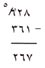استعمل الأسلوب نفسه مع الآلاف، أي استلف 1000 تماماً كما استلفت 10 أو 100.

التَحقُّق من الطرح

يجب عليك دائماً التحقق من عملك في الطرح للتأكد من أنك قمت به بالشكل الصحيح.

التحقق باستخدام الطرح:

إحدى طرق التحقق من مسألة الطرح هي أن تطرح الباقي من المطروح منه .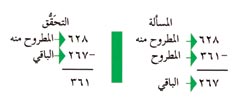

يجب أن يكون الباقي الجديد هو نفس المطروح القديم، بهذا يمكن أن تتحقق من جوابك.

التحقق باستخدام الجمع:

من الطرق الجيدة للتحقق من مسألة الطرح، التحقق بواسطة الجمع، لأن الجمع عكس الطرح. اجمع المطروح والباقي: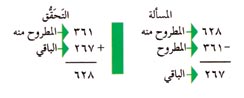

يجب أن يكون ناتجُ الجمع هو نفس المطروح منه القديم في مسألة الطرح.

التخمين أو التقدير:

يساعدك لتعرف فيما إذا كان جوابك منطقياً. حاول تخمين الجواب قبل أن تحل المسألة. إليك هذا المثال:

وغالبا مايكون هذا هو الجواب الفعلي.

وتستطيع التقدير بأعداد أكبر. على سبيل المثال 476 تساوي حوالي 500 و 254 تساوي حوالي 250، اطرح 500-250 يعطيك 250. يعطيك هذا فكرة جيدة عن الجواب. وسيوفر لك تقدير الجواب الوقت قبل حلِّك للمسألة إذا ما ارتكبت خطأ، لأنك تعرف الجواب سلفًا.

حقائق الطرح الواجب تذكرها

1 - تذكَّر ماذا يعني الطرح، تستطيع أن تجد الإجابات لمسائل الطرح عن طريق العد، لكن من الأسرع والأسهل أن تفكَّر في الإجابات.

2 - تعلُّم حقائق الطرح سيساعدك على التفكير في الإجابات لمسائل الطرح بسرعة.

3 -الطرح هو عكس الجمع. ولهذا السبب سيساعدك الجمع على تعلُم حقائق الطرح والتحقق من حل المسائل.

4 - ستساعدك حقائق الطرح على طرح أعداد أكبر لحل المسائل.

5 - تستطيع أن تطرح فقط كميات من نفس النوع، أي يجب أن تطرح آحادًا من آحاد وعشرات من عشرات.

6 - يجيب الطرح عن ثلاثة أنواع من الأسئلة: كم الباقي؟ مالفرق؟ وكم شيئاً آخر نحتاج؟

طرق أخرى للطرح

هناك عدة طرق للتفكير في مسألة الطرح. تُسمى الطريقة التي سبق استخدامها طريقة الاستلاف والاستبعاد، وهذا مثال آخر :

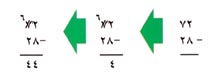واضح أنك لاتستطيع أخذ 8 آحاد من اثنين. استلف 10 مما يجعل المطروح منه 6 عشرات واثني عشر من الآحاد. ثم اطرح 8 آحاد من اثني عشر من الآحاد: 12 - 8 = 4. اكتب الأربعة في خانة الآحاد من الجواب. بعد ذلك اطرح عشرتين من 6 عشرات: 6 - 2 = 4 اكتب الأربعة في خانة العشرات من الجواب.

وهناك طريقة أخرى تُسمى طريقة الجمع والاستلاف.

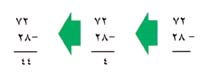الأعداد هي نفسها كما في طريقة الاستلاف والاستبعاد لكن التفكير يختلف. ترى أنك لاتستطيع أخذ 8 آحاد من اثنين، فتستلف 10 وبدلاً من طرح 8 آحاد من اثني عشر من الآحاد تُفكّر ¸ما الذي يُضاف إلى 8 فيجعلها 12·؟ إنك تعرف أن 8 + 4 = 12، لذلك اكتب الأربعة في خانة الآحاد من الجواب. وبدلاً من أن تطرح عشرتين من 6 عشرات تُفكر ¸ما الذي يضاف إلى 2 فيجعلها 6·؟ إنك تعرف أن 2 + 4 = 6 لذلك اكتب الأربعة في خانة العشرات من الجواب.

وتسمى طريقة ثالثة طريقة الجمع والحمل أو الطريقة النمساوية:

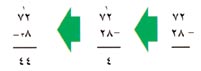أولاً: يتضح لك أنك لاتستطيع أخذ 8 آحاد من اثنين. وبدلاً من الاستلاف اجمع 10 آحاد إلى الاثنين:

2 + 10=12 ثم فكر ¸ما الذي يضاف إلى 8 فيجعلها 12·؟ إنك تعرف مُسبقاً أن 8 + 4 = 12 لذلك اكتب الأربعة في خانة الآحاد من الجواب. فكر الآن ¸لقد أضفت 10 إلى الآحاد لذلك يجب أن أطرح 10 من العشرات·. ولعمل ذلك حول العشرين في المطروح إلي 3 عشرات.

فكر ¸ما الذي يضاف إلى (يجمع إلى) 3 فيجعلها 7·؟ إنك تعرف أن 3 + 4 = 7 لذلك اكتب الأربعة في خانة العشرات من الجواب.

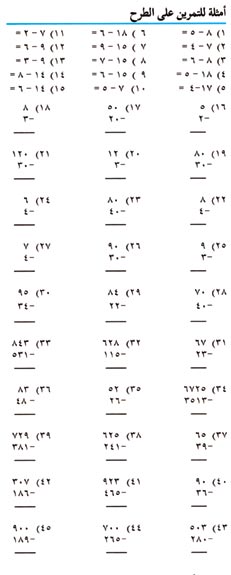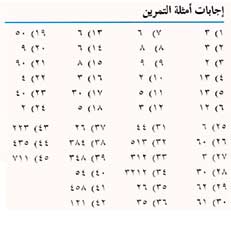التسلية بالطرح

كي نلعب لعبة تُسمى أكثر أو أقل ضع رزمة من 36 بطاقة، واكتب عليها الأعداد من 1 إلى 18 بشكل منفرد في مجموعتين فسيكون هناك بطاقتان لكل عدد، اخلط البطاقات واجعل وجه الكومة لأسفل، فيأخذ قائد اللعبة بالبطاقة الأولى ويرفعها ليراها اللاعبون، افرض أنها 14، ثم يأخذ اللاعب الأول بطاقة من الكومة ويعرضها، افرض أنها 6 فيقارنها اللاعب مع البطاقة المكتوب عليها 14 ويقول ¸إنها أقل· ثم يُحدِّد بكم تقل عن 14. في هذه الحالة يجب أن يقول اللاعب ¸إنها تقل عن 14 بـ 8· يجب عليه أن يجد الجواب بالتفكير في الطرح. افترض أن اللاعب الثاني قلب بطاقة كُتِب عليها 17 فيقارنها بالبطاقة الأولى، يجب أن يقول ¸إنها أكثر من 14 بـ 3·. وعلى اللاعب الذي يعطي إجابة خاطئة الخروج من اللعبة. فإذا انتهيتم من البطاقات مرة واحدة، يمكنكم خلطها ثانية واللعب بها مرة أخرى بأعداد جديدة.