في الرياضيات، يستعمل نظام الإحداثيات الديكارتية لتحديد نقطة في مستوي عبر عددين، يطلق عليهما عادة الإحداثية-س و الإحداثية-ص. لتعريف الإحداثيات، نقوم بإسقاط خطين عموديين (محور السينات أو س و محور الصادات أو ص)، كما يجب كذلك تعريف وحدة الطول، و التي نبيّنها على المحورين (أنظر الصورة 1).
تستعمل أنظمة الإحداثيات الديكارتية في الفضاء أيضا (باستعمال ثلاث إحداثيات)، أو حتى في أبعاد أكثر.
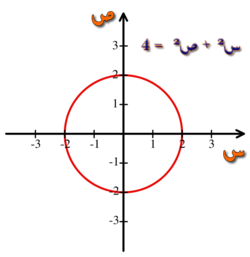
باستعمال نظام الإحداثيات الديكارتية، يمكن التعبير عن الأشكال الهندسية باستعمال معادلات جبرية، و هي معادلات توافق إحداثيات النقاط الممثّلة للشكل الهندسي. فعلى سبيل المثال، يعبّر عن دائرة ذات شعاع مساو لـ2، بالمعادلة التالية س² + ص² = 4. (أنظر الصورة 2).
سمي النظام بالـديكارتي تبعا للرياضي و الفيلسوف الفرنسي ريني ديكارت (كارتيسيوس باللاتينية)، و الذي عمل على ادماج الجبر و الهندسة الإقليدية. كان هذا العمل حاسما في مجال الهندسة التحليلية و دراسة الدوال و الخرائط.
تم تطوير فكرة النظام هذه سنة 1637، في كتابتين مختلفتين لديكارت. في الجزء الثاني من حديث الطريقة، يقدّم ديكارت فكرته الجديدة لتحديد موقع نقطة أو شكل على المستوي، باستعمال محورين متقاطعين كآداة للقياس. و في الهندسة، يكشف ديكارت أكثر عن المفاهيم التي سبق ذكرها.
فهرس |
نظام الإحداثيات ثنائي الأبعاد
يعرّف نظام الإحداثيات الديكارتي الحديث ذو البعدين عادة بمحورين، يشكلان مستو (مستوي-س،ص). يعنون المحور الأفقي عادة بـ س، و العمودي بـ ص. أما في النظام ذو الأبعاد الثلاث، يتم إضافة محور ثالث، يسمى عادة ز، مما يضيف بعدا ثالثا للقياس. تختار المحاور عادة متعامدة بعضها مع بعض. تسمى المعادلات التي تستخدم الإحداثيات الديكارتية، معادلات ديكارتية.
يسمى تقاطع المحاور، بالنقطة الأصل و تسمى عادة م. يحدد محوري السينات و الصادات مستو يعرف بمستوى السينات-الصادات. كما يجب إختيار وحدة طول، و الإشارة إليها على المحورين، لتشكيل شبكة. لتحديد نقطة ما في نظام ديكارتي ثنائي الأبعاد، حدد إحداثية السين أولا (س) ثم إحداثية الصاد (ص) في شكل زوج مرتّب (س،ص).
على سبيل المثال النقطة أ في الصورة 3، باستعمال الإحداثيات (3،5).
يحدد تقاطع المحورين أربع مناطق، يشار إليها بالأرقام الرومانية I (+,+) و II (−,+) و III (−,−) و IV (+,−). اتفاقا، ترقم هذه المناطق عكس عقارب الساعة ابتداءا من المنطقة اليمنى العليا. في المنطقة الأولى، تكون كلا الإحداثيتين موجبتين، أما في الثانية، فتكون إحداثية السين سالبة و إحداثية الصاد موجبة، أما في المنطقة الثالثة تكون كلاهما سالبتين، و أخيرا في المنطقة الرابعة تكون إحداثية السين موجبة و إحداثية الصاد سالبة.(أنظر الصورة 3).
نظام الإحداثيات ثلاثي الأبعاد
يوفّر نظام الإحداثيات ثلاثي الأبعاد، الأبعاد الفيزيائية الثلاث : الطول، العرض، الإرتفاع. تبيّن الصورتان 4 و 5، طريقتين معتمدتين لعرض نظام إحداثيات ثلاثي الأبعاد.
تكون الإحداثيات في النظام الثلاثي الأبعاد على شاكلة (س،ص،ز). و على سبيل المثال، تم تصوير نقطتين في نظام الصورة 4، النقطة أ(3،0،5) و النقطة ب(-5،-5،7).
يمكن كذلك إستنتاج إحداثيات الس، و الص، و الز من الأبعاد عن المستوي ص،ز و المستوي س،ز و المستوي س،ص. تبيّن الصورة 5 أبعاد النقطة أ عن المستويات.
تقسّم محاور النظام الثلاثي الأبعاد الفضاء إلى ثمان مناطق شبيهة بمناطق النظام ثنائي الأبعاد.
في الفيزياء
ينطبق ما سبق على نظام الإحداثيات الديكارتية في الرياضيات، حيث من العادي أن لا تستعمل أي وحدة للقيس. ولكن، من الضروري أن نؤكد أن الأبعاد في الفيزياء هي ببساطة قيس لشيء ما، و أنه قد يكون من الضروري أيضا إضافة بعد آخر. إن الأشياء متعددة-الأبعاد يمكن أن نحسبها و نتحكم بها جبريا.
تمثيل متّجه بكتابات ديكارتية
يمكن كذلك التعبير عن نقطة في نظام إحداثيات ديكارتي بمتجه، الذي يمكن تصويره على أنه سهم منطلق من النقطة الأصل و مشير إلى تلك النقطة. إذا كانت الإحداثيات تعبّر عن مواقع فضائية، من المتعارف عليه تصوير المتجه من الأصل إلى النقطة بـ 
. و باستعمال الإحداثيات الديكارتية يكتب المتجه من الأصل إلى النقطة (x,y,z) :
حيث 
و 
و 
هي متجهات وحدة تشير إلى نفس اتجاهات محاور الـ x و y و z، على الترتيب.