الرئيسيةبحث

توزيع احتمالي طبيعي

التوزيع الطبيعي
دالة الكثافة الاحتمالية
دالة الكثافة الاحتمالية للتوزيع الطبيعي
الخط الأخضر يمثل التوزيع الاحتمالي الطبيعي الموسّط المختزل
دالة التوزيع التراكمي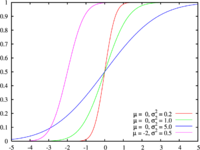
دالة التوزيع التراكمي للتوزيع الاحتمالي الطبيعي
المؤشرات μ موقع (عدد حقيقي)
σ2 > 0 مقياس تربيعي ( عدد حقيقي )
الدعم x \in ]-\infty;+\infty[ \!
د.ك.ا \frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!
د.ت.ت \frac12 \left(1 + \mathrm{erf}\,\frac{x-\mu}{\sigma\sqrt2}\right) \!
المتوسط الحسابي μ
الوسيط الحسابي μ
المنوال μ
التباين σ2
الميلان الاحصائي 0
الكورتوسيس 3 (حالة توزيع طبيعي)

0 (في حالة توزيع طبيعي موسّط ومختزل)
الاعتلاج \ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!
د.م.ع M_X(t)= \exp\left(\mu\,t+\sigma^2 \frac{t^2}{2}\right)
الدالة المميزة \phi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)


التوزيع الطبيعي الموسّط المختزل

الدالّة \varphi : \R \to \R^+ بحيث \varphi(t)=\frac{1}{\sqrt{2\;\pi}}\, \mathrm{e}^{-\frac{t^2}{2}}

هي دالة كثافة احتمالية : هي متواصلة وتكاملها على \ \R يساوي 1.

فاننا نعلم أن \ \int_{-\infty}^{+\infty}\mathrm{e}^{-\frac{t^2}{2}}\ dt = \sqrt{2\, \pi} (تكامل غاوس).

ونبين أن (أنظر التالي) التوزيع الذي يقع تحديده انطلاقا من دالة الكثافة هذه له قيمة متوقعة تساوى 0 وتباينا يساوي 0.

ملاحظات

التعريف

نسمي التوزيع الطبيعي (أو غاوسي) موسّط مختزل التوزيع المعرّف بدالة الكثافة \varphi.

الرسم البياني لهذه الكثافة يمثل شكل جرس.

دالة التوزيع التراكمي

لتكن Φ دالة التوزيع التراكمي (Cumulative distribution function-Fonction de répartition) للتوزيع الموسّط المختزل. تحدد لكل عدد حقيقي x ب:

\ \Phi(x) = \int_{-\infty}^x \varphi(t)\, dt = \int_{-\infty}^x\frac{1}{\sqrt{2\,\pi}}\,\mathrm{e}^{-\frac{t^2}{2}}\, dt .

وهي تكامل \varphi ونهايتها في -\infty تساوي 0، ولا يمكن كتابتها باستعمال الدالات المعروفة (أس، جيب..) ولكن تصبح هي بنفسها دالة مستعملة بكثرة ومهمّة لكلّ من يمارس حساب الاحتمالات والإحصاء.

خاصيات الدالة Φ :