المثلث ( Triangle )
المثلث شكل محاط بثلاثة مستقيمات تسمى الأضلاع. وتتقابل الأضلاع في ثلاث نقاط تسمى الرؤوس، ويشكل كل رأس مع ضلعيه زاوية من زوايا المثلث، ومجموع زوايا المثلث الثلاث يساوي دائماً 180°. والمثلث هو أحد أنواع المضلع ★ تَصَفح: المضلع.
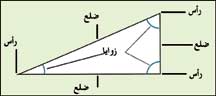 |
أجزاء المثلث المثلث شكل مستو له ثلاثة أضلاع وثلاث زوايا. وتتقابل الخطوط المستقيمة التي تمثل أضلاع المثلث في ثلاث نقاط تُسمى الرؤوس. ويشكل كل رأس مع ضلعيه المحيطين زاوية من زوايا المثلث. |
أنواع المثلثات:
يمكن تصنيف المثلثات حسب العلاقة بين أضلاعها. فالمثلث المختلف الأضلاع له ثلاثة أضلاع مختلفة الأطوال. أما المثلث المتساوي الساقين فله ضلعان متساويان من أضلاعه الثلاثة. ويسمى المثلث الذي تتساوى أطوال جميع أضلاعة الثلاثة المثلث المتساوي الأضلاع. ومن هنا، فإن كل مثلث متساوي الأضلاع هو مثلث متساوي الساقين، ولكن العكس ليس صحيحاً، فليس كل مثلث متساوي الساقين متساوي الأضلاع.يمكن تصنيف المثلثات حسب زواياها. فالمثلث الذي تكون كل زاوية من زواياه أصغر من 90°هو مثلث حاد الزوايا، أما المثلث المنفرج الزاوية فهو مثلث تكون إحدى زواياه أكبر من 90°. والمثلث الذي تكون إحدى زواياه 90°يسمى المثلث القائم الزاوية.
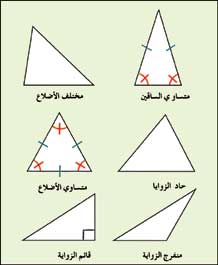 |
أنواع المثلثات يمكن تصنيف المثلثات بزواياها وحسب العلاقة بين أضلاعها. وفي الشكل المرفق، تمثل الخطوط الزرقاء أضلاعًا متساوية الطول في المثلث، أما الرموز الحمراء فتمثل زوايا متساوية. ويمثل الصندوق الصغير، ذو اللون الرمادي زاوية قائمة أي زاوية تساوي 90°، والمثلث القائم الزاوية هو الذي تكون إحدى زواياه قائمة (أي 90°) ولا يمكن أن يكون في أي مثلث أكثر من زاوية واحدة قائمة أو منفرجة. |
خواص وعلاقات المثلثات:
هناك خواص وعلاقات متعددة بين أجزاء المثلث. ويمكن كذلك إيجاد علاقة مفيدة بين مثلثين أو أكثر في بعض الأحيان. وستتم مناقشة بعض هذه الخواص والعلاقات هنا كالتالي.المحيط والمساحة. محيط المثلث هو مجموع أطوال أضلاعه. ولإيجاد مساحة المثلث ينبغي أن نعرف ارتفاعه وهو المسافة العمودية بين أحد رؤوس المثلث والضلع المقابل أي القاعدة. ولإيجاد المساحة تضرب القاعدة في الارتفاع ثم يقسم الناتج على 2. ومن هنا، حتى لو تساوت محيطات عدد من المثلثات، فإن مساحاتها قد تكون مختلفة.
المثلث القائم الزاوية ونظرية فيثاغورث. هناك علاقة خاصة بين أضلاع المثلث القائم الزاوية. ويتم التعبير عن هذه العلاقة بوساطة قانون رياضي يسمى نظرية فيثاغورث ★ تَصَفح: فيثاغورث، نظرية. كانت هذه النظرية معروفة في الحضارات القديمة، ولكنها تنسب إلى عالم الرياضيات والفيلسوف اليوناني فيثاغورث. تنص نظرية فيثاغورث على أن المثلث يكون قائم الزاوية إذا كان مجموع مربعي طولي ضلعيه القصيرين مساوياً لمربع طول ضلعه الأطول الذي يسمى الوتر. ويمكن كتابة هذه العلاقة باستخدام الصيغة ا²+ ب² = جـ². وعلى سبيل المثال، لو كانت أطوال أضلاع مثلث ما هي 6 و 8 و10 فإن هذا المثلث مثلث قائم الزاوية لأن 6² + 8²= 10² (36+ 64= 100). وتمكننا هذه الصيغة من حساب طول أي ضلع من أضلاع المثلث القائم الزاوية إذا عرفنا طولي الضلعين الآخرين.
التطابق. يكون المثلثان متطابقين، أي لهما نفس الشكل والمساحة بالضبط، إذا كانت أضلاعهما وزواياهما المتناظرة متساوية. وقد قام علماء الرياضيات بصياغة مجموعات محددة من الشروط لتحديد التطابق. وعلى سبيل المثال، فإن أي مثلثين يكونان متطابقين إذا تساوت أضلاعهما المتناظرة. ولو رمز للضلع بالرمز (ض)، يمكن اختصار العبارة السابقة على النحو: ض ض ض= ض ض ض. وتشمل بعض المجموعات الأخرى من شروط التطابق زوايا المثلث وأضلاعه على حدٍ سواء. فلو كان الرمز (ز) يدل على الزاوية، فإن المجموعة الأخرى من الشروط هي:
ز ز ض = ز ز ض، ض ز ض = ض ز ض، ز ض ز = ز ض ز.
التشابه. يكون المثلثان متشابهين إذا تساوت زواياهما المتناظرة أوكانت أطوال أضلاعهما المتناظرة متناسبة ـ كأن يكون طول كل ضلع في أحد المثلثين مساوياً لنصف طول الضلع المناظر في المثلث الآخر. ولهذا يكون للمثلثات المتشابهة نفس الشكل مع أن مساحات هذه المثلثات ليست متساوية بالضرورة. وعلى سبيل المثال، لو كانت أطوال أضلاع مثلث ما هي 3، 4 ، 5 وأطوال أضلاع مثلث آخر هي 6، 8 و10، فإن أطوال الأضلاع تكون متناسبة ويكون المثلثان متشابهين.
وكما في تطابق المثلثات، يمكن معرفة أوضاع تشابه المثلثات بدون معرفة جميع الزوايا والأضلاع. فلو تساوى كل زوجين متناظرين من الزوايا مثلاً كان المثلثان متشابهين. وبالمثل لو كانت الأضلاع الثلاثة للمثلثين متناسبة فإن المثلثين يتشابهان كذلك. وفي المثلث القائم الزاوية، يقسم الارتفاع ـ وهو المستقيم العمودي من رأس الزاوية القائمة إلى الوتر ـ المثلث إلى مثلثين متشابهين ومشابهين للمثلث الأصلي.