فيثاغورث، نظرية ( Pythagoras' theorem )
فيثاغورث، نظرية. تنص نظرية فيثاغورث في علم الهندسة أنه ¸في المثلث القائم الزاوية يكون مربع الوتر مساويًا لمجموع مربعي الضلعين الآخرين·. والمثلث القائم الزاوية هو المثلث الذي تكون إحدى زواياه قائمة، أي تساوي 90°، والوتر هو الضلع المقابل للزاوية القائمة، وتصاغ النظرية في المعادلة التالية:
أ² + ب² = جـ²
في هذه المعادلة يرمز أ إلى طول الوتر بينما يرمز كل من ب و جـ للضلعين الآخرين في المثلث. فإذا عرفت طولي أي ضلعين في المثلث القائم الزاوية يمكن التعويض عن مقداريهما في المعادلة واستخراج طول الضلع الثالث.
نشأة النظرية:
أراد قدماء المصريين أن يخططوا أركانًا قائمة الزاوية لحقولهم، ولم تكن لديهم الأدوات المتوفرة اليوم. فكيف يصنعون زاوية قائمة 90°؟ اكتشف المصريون حوالي سنة 2000 ق.م، المثلث السحري 3-4-5 فأعدّ العمال حبلاً به 12 عقدة بينها مسافات متساوية، وشدوا الحبل حول ثلاثة أوتاد لتكوين مثلث أطوال أضلاعه 3، 4، 5 وحدات. وضلع المثلث ذو الوحدات الخمس هو الذي نطلق عليه الوتر، وتقابله الزاوية التي مقدارها90°.تعلم الإغريق القدماء هذا العمل البارع من المصريين. وفي الفترة من سنة 500 حتى 350 ق.م. اكتشفت مجموعة من الفلاسفة الإغريق يدعون الفيثاغورثيين (أتباع فيثاغورث) المثلث 3-4-5. وتعلموا فكرة أن أضلاع المثلث القائم الزاوية هي جوانب لثلاث مربعات. وتساوي مساحة المربع طول ضلعه مضروبًا في نفسه. وفي المثلث 3-4-5 تساوي مساحة المربع الذي يكون الوتر أحد أضلاعه، مساحة مجموع مربعي الضلعين الآخرين 5×5=3×3+4×4. ثم عمم الفيثاغورثيون هذه القاعدة عن المثلث 3-4-5 لكي يطبقوها عمليًا على كل المثلثات القائمة الزاوية، وأصبح هذا المبدأ العام معروفًا بنظرية فيثاغورث.
برهان إقليدس:
تضمنت المصطلحات الهندسية عدة براهين على نظرية فيثاغورث. وينسب أحد هذه البراهين الشهيرة إلى عالم الرياضيات الإغريقي إقليدس. وفي الرسم أدناه تمثل أ ب جـ المثلث القائم الزاوية الأصلي ورسمت مربعات على كل ضلع من أضلاع المثلث، وتحددت الزاوية القائمة في جـ. فكيف تثبت أن المربع على الوتر يساوي مجموع مربعي الضلعين الآخرين؟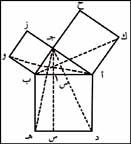 |
برهان إقليدس |
فيما يلي خطوات البرهان. تنبع أسباب كل خطوة من البدهيات والمبادئ وغيرها من النظريات الهندسية.
أولاً يمكنك باستخدام سلسلة من الخطوات إثبات أن مساحة المربع المقام على الضلع أجـ تساوي ضعف مساحة المثلث أ ب ك.
ثانيًا: المثلثان أ ب ك ، أ جـ د متطابقان.
ثالثًا: مساحة المستطيل أ د س س1 تساوي ضعف مساحة المثلث أ جـ د. وبناءً عليه فإن مســـاحة المربع المقام على الضلع أ جـ تساوي مساحة المستطيل أ د س س1.
وبالطريقة نفسها يمكن إثبات أن مساحة المربع المنشأ على الضلع ب جـ يساوي مساحة المستطيل ب هـ س س1. وأخيرًا فإن مربع الضلع أ ب يساوي حاصل جمع أجزائه (أ د س س1) و (ب هـ س س1)، أي مجموع المربعين المقامين على الضلعين الآخرين.