الكسر ( Fraction )
☰ جدول المحتويات
الكسـر جزء من شيء ما. وعندما تقاس الأشياء، فغالبا لا يساوي الناتج وحدات كاملة. فقد يزن كتاب ما بين اثنين وثلاثة كجم، فما زاد عن كيلوجرامين يكون كسرًا لكيلو جرام. ويمكن أن يتراوح طول لوحة بين 10 و11 سم فيكون طولها 10 سم زائدًا كسرًا للسنتيمتر.
تنتج الكسور من تقسيم وحدة إلى عدد من الأجزاء المتساوية. ويمكن تقسيم الوحدة إلى أي عدد من الأجزاء. فإذا كسرت عصا إلى قطعتين، فلن تحصل بالضرورة على نصفين للعصا. وللحصول على نصفين للعصا، عليك أن تكسرها لقطعتين متساويتي الطول.
تكتب الكسور بصورة عددية على شكل عددين يفصلهما خط على النحو :
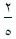 |
ويمثل الكسر عمومًا، في الحساب، عدد الأجزاء المتساوية التي قُسِّمّ لها شيء ما، أو عدد الأجزاء التي أخذت في الاعتبار، على سبيل المثال، يمثل الكسر 2/5 جزءين من شيء قسّم إلى خمسة أجزاء متساوية.
تستخدم صيغة الكسر أيضا لأجل 1- التعبير عن قسمة، 2- تمثيل نسبة، 3- الدلالة على معدّل. وللتعبير عن القسمة، يمكن أن يشير الكسر 2/5 إلى قسمة 2 على 5، كتقسيم قطعتين من الحلوى بالتساوي على خمسة أشخاص مثلاً. أما النسبة فهي مقارنة بين كميتين قيستا بنفس الوحدات. ويمكن للنسبة أن تقارن جزءًا إلى الكل أو جزءًا إلى جزء آخر. مثلا، إذا كان فريق مناظرة مؤلفًا من بنتين وثلاثة أولاد، فتكون نسبة البنات، وهو جزء، إلى أعضاء الفريق، وهو الكل، 2 إلى 5 أو 2/5. وتكون نسبة البنات، كجزء، إلى الأولاد، كجزء آخر، 2 إلى 3 أو 2/3. يسمى أي عدد في الرياضيات، عددًا منطقيًا أو قياسيًا إذا أمكن كتابته على شكل نسبة عددين صحيحين. ★ تَصَفح: النسبة. ولا يمكن كتابة الأعداد غير النسبية كنسبة لعددين صحيحين.
فالعدد ط (باي) الذي يعرف بأنه نسبة محيط دائرة إلى طول قطرها، هو عدد غير نسبي. ولكن الكسر يعطي قيمة تقريبية للعدد باي، يمكن استخدامها في الحسابات ★ تَصَفح: ط باي. أما المعدّل فهو العلاقة بين كميتين قيستا بوحدات مختلفة. على سبيل المثال، يمكن لفريق كرة سلة أن يسجل أهدافًا بمعدل هدفين في كل خمس دقائق من اللعب.
والمعاني والاستخدامات المختلفة للكسور جد مرتبطة. وغالبًا ما يساعد فهم أحد معاني الكسور على فهم الاستخدامات الأخرى بسهولة. وتركز هذه المقالة على معنى الكسور كأجزاء من كل، وتنظر في استخدام الكسور في الحساب.
| مصطلحات الكسور | ||||||||||||||||||||||||||||
|
التعبير عن الكسور
 |
التعبير عن الكسور بالكلمات |
التعبير بالكلمات:
تشتق الكسور مسمياتها من عدد الأجزاء المتساوية التي قسُمِّت إليها الوحدة الكاملة. وتوجد في اللغة أسماء خاصة للدلالة على الأجزاء الكسرية الناتجة عندما تقسّم الوحدة إلى جزءين متساويين أو ثلاثة أجزاء أو أربعة أو... حتى عشرة أجزاء متساوية. وعندما تقسم وحدة إلى جزءين متساويين يدعى كل جزء نصفا، وعندما تقسم إلى ثلاثة أجزاء متساوية يدعى كل جزء ثلثًا، وهكذا ربعًا وخمسًا وسدسًا وسبعًا وثمنًا وتسعًا وعشرًا.وكلما قسمت الوحدة إلى عدد أكبر فأكبر من الأجزاء المتساوية أصبح الجزء أصغر فأصغر. وإذا قسمت وحدة إلى خمسة أجزاء متساوية يكون الجزء الواحد خمسًا. وإذا قسمت الوحدة ذاتها إلى عشرة أجزاء متساوية يكون الجزء الواحد عشرًا. ومع أنه قد يبدو أن العشر أكبر من الخمس، إلا أن العشر يساوي نصف الخمس.
وتدل كلمة العدد التي تسبق الكسر على عدد مرات أجزاء الكسر المأخوذة بالاعتبار. مثلا، خمسة أسداس تمثل خمسة من الأسداس الستة التي قسم لها شيء ما، وستة أسداس تعني أن وحدة قسمت لستة أجزاء متساوية وأن جميع الأسداس الستة أخذت في الاعتبار. وعليه فإن ستة أسداس تساوي وحدة واحدة كاملة. وبالمثل سبعة أسباع وثمانية أثمان وتسعة أتساع، وهكذا جميعها تساوي واحدا.
التعبير بالرموز:
عندما تكتب الكسور بشكل عددي، يسمّى العدد الموجود في الأسفل، أو الثاني، المقام. وهو يزود الكسر بالاسم، ويخبر عن عدد الأجزاء المتساوية التي قسمت لها الوحدة. ويسمّى العدد الموجود في الأعلى، أو الأول، البسط ونطلق على البسط والمقام حدّي الكسر.وتسمى الكسور ، مثل 4/10، 7/100، 5/1000 كسورًا عشرية أي الكسور التي مقاماتها 10 أو 10 مضروبة في نفسها عددا من المرات. ويمكن باستخدام النظام العشري كتابة الكسور العشرية بدون مقام. وفي هذا النظام، تكون قيمة كل خانة عشرية في الرقم أصغر بعشر مرات من تلك التي إلى يسارها مباشرة. فمثلا الموضع الأول إلى يمين الفاصلة العشرية هو موضع الأعشار أو أجزاء العشرة، والثاني إلى يمين الفاصلة هو موضع أجزاء المائة. ويدل عدد الخانات العشرية المستخدمة في النظام العشري على عدد الأجزاء التي تكون الوحدة قد قسمت لها. وتمثل الأرقام الموجودة في الخانات العشرية عدد وحدات الأجزاء المأخوذة بالاعتبار. مثلا، يمكن كتابة الكسر 7/10 بالنظام العشري على الشكل 0,7 وكتابة سبعة وعشرين جزءًا من مائة 0,27 وللحصول على معلومات عن تحويل الكسور إلى عشرية والعشرية إلى كسور. ★ تَصَفح: النظام العشري.
| معاني مختلفة لرمز الكسر 2/5 | |||||||||||||||
|
الكسور المتكافئة
 |
الكسـور المتكافئـة |
ويمكن أن يكون البسط في عدة كسور مختلفا وكذلك المقام، غير أن الكسور تبقى ممثلة لنفس الجزء من الوحدة الكاملة. وتسمى مثل هذه الكسور كسورًا متكافئة. ويوضح الرسم وحدة قسمت إلى أجزاء كسرية مختلفة. ويوضح أيضًا عدة مجموعات لأجزاء كسرية مكافئة لـ 1/2 و 1/3 و 1/4 فمثلا، يعبر 1/2 عن نفس الجزء من الوحدة الذي تعبر عنه مجموعة مؤلفة من ربعين 2/4 أو من خمسة أعشار، 5/10. ولهذا السبب تكون الكسور 1/2 و 2/4 و 5/10 متكافئة.
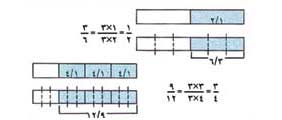 |
الضرب لإيجاد الكسور المتكافئة هو كتقسيم جزء كسري إلى أجزاء أصغر. فمثلا، ضرب بسط ومقام 1/2 في 3 يعطي 3/6، وهذا يعبر عن نفس الجزء من الكل كما يفعل 1/2. وتعادل هذه العملية عملية تقسيم 1/2 إلى ثلاثة أجزاء متساوية. |
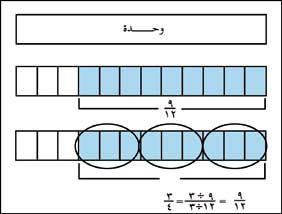 |
التقسيم لايجاد الكسور المتكافئة، ويطلق عليها "اختزال الكسور" مثلاً: تقسيم بسط ومقام 9/12 على 3 يعطي 3/4. وتشبه هذه، تجميع تسعة 1/12 على شكل ثلاث مجموعات في كل منها ثلاثة 1/12. تساوي كل مجموعة من ثلاثة 1/12 ، 1/4. |
ويعادل تقسيم كل جزء إلى كسر إلى مزيد من أجزاء متساوية، عملية ضرب بسط ومقام ذلك الكسر في نفس العدد، والذي يؤدي إلى كسر، مكافئ للأول، بسطه ومقامه أكبر من بسط ومقام الكسر الأول.
اقسم بسط ومقام كسر على عدد واحد لتحصل على كسر مكافىء بسطه ومقامه أصغر من بسط ومقام الكسر الأول.
(6 ÷ 2) / (12 ÷ 2) = 3/6
(5 ÷ 5) / (10 ÷ 5) = 1/2
تسمى عملية ايجاد كسر مكافئ ذي أعداد أصغر في البسط والمقام، اختصار الكسر. عندما لا يوجد عدد، عدا الواحد، يمكن استخدامه لتقسيم البسط والمقام عليه، فيقال بأن الكسر قد اختصِر لأدنى الحدود.
مقارنة الكسور
عندما يتساوى مقاما كسرين، يمكن بسهولة معرفة أي الكسرين أكبر، فأكبرهما هو ذو البسط الأكبر لأنه يشمل أجزاء أكثر من نفس الوحدة.
فمثلا 5/7 من شيء ما، أكبر من 3/7 من الشيء ذاته.
أما إذا اختلف المقامان فتزداد صعوبة تحديد أي الكسرين أكبر. عندها يلزم تحويل الكسور إلي كسور متكافئة، وهو ما يسمى بعملية إيجاد المقام المشترك. وإحدى الطرق السهلة لإيجاد المقام المشترك هو ضرب أحد المقامين في الآخر ثم استخدام الناتج كمقام مشترك. مثلا، كي نحدد أي الكسرين 1/2 أو 3/7 أكبر، اضرب المقامين ببعض لتجد أن المقام المشترك 2 × 7 =14، اضرب بسط ومقام 1/2 في 7 كي تحوله إلي كسر مكافئ له، وذلك لأن 7 × 2 = 14.
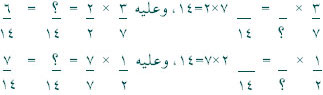 |
وعليه، يكون 3/7 مساويا 6/14، ويكون 1/2 مساويا 7/14
ولأن 7/14 أكبر من 6/14 فيكون 1/2 أكبر من 3/7
ويمكن التفكير بهذه الطريقة لإيجاد مقام مشترك على أنها عملية ضرب بسط ومقام كل كسر بمقام الكسر الآخر.
استخدام الكسور في العمليات الحسابية
جمع وطرح الكسور:
عملية يمكن القيام بها فقط عندما تكون للكسور نفس المقام. وعندما تكون المقامات متساوية فهي تشير إلى أجزاء متساوية من الكل، إذ يمكن جمع أسباع لأسباع لتحصل على أسباع ويمكن طرح أثلاث من أثلاث لتحصل على أثلاث. لكن لا يمكن جمع أسباع وأثلاث، أو طرح أثلاث من أسباع دون القيام أولاً ببعض الحسابات الإضافية.كي تجمع أو تطرح كسرين لهما مسبقا نفس المقام، أضف البسط للبسط أو اطرح البسط من البسط، دون تغيير المقام ؛ سيكون المقام في الجواب هو نفس المقام في كسري المسألة. وعند جمع أو طرح الكسور يتغير العدد الإجمالي للأجزاء الكسرية، ولكن قياس كل من هذه الأجزاء لا يتغير.
2/6 + 3/6 = 5/6 ، 7/8 - 5/8 = 2/8
كي تجمع أو تطرح كسرين لهما مقامان مختلفان، حوِّل أولا الكسرين إلى كسرين متكافئين له بحيث يكون للكسرين الجديدين مقام مشترك، كما في المثال التالي، ثم اجمع أو اطرح.
2/3 - 1/2 = (2×2)/(3×2) - (1×3)/(2×3) =4/6 - 3/6 = 1/6
 |
طريقتان لضرب الكسور |
ضرب الكسور:
يشبه ضرب الكسور ضرب الأعداد الصحيحة. ويمثل تكرار الجمع أحد معاني الضرب.3 × 4 تعني 4 + 4 + 4 أو ثلاث مجموعات من 4.
3 × 1/2 تعني 1/2 + 1/2 + 1/2 أو ثلاث مجموعات من 1/2، أو ثلاثة أنصاف.
يكون الناتج في حالة ضرب الأعداد الصحيحة الموجبة أكبر من العددين الأصليين، ولكن الناتج في حالة ضرب كسر في كسر، يكون أصغر من الكسر الأصلي وذلك لأنك تحصل على مجرد جزء منه.
2/3 × 4/5 تعنى 2/3 من 1/5 + 2/3 من 1/5 + 2/3 من 1/5 + 2/3 من 1/5
أو 2/3 من مجموعة أربعة أخماس، أو 2/3 من 4/5
يمثل الكسر 4/5 أربعة أجزاء من تلك الأجزاء الناتجة عن تقسيم وحدة إلى خمسة أجزاء متساوية. وتعنى المسألة 2/3× 4/5 أخذ 2/3 من كل من تلك الأخماس الأربعة. نستطيع أن نجد 2/3 لـ 1/5 بتقسيم 1/5 إلى ثلاثة أجزاء متساوية وأخذ اثنين منها. وعندما تقسم وحدة واحدة إلى خمسة أجزاء متساوية، 1/5، وتقسم كل من هذه الأجزاء الخمسة إلى ثلاثة أجزاء متساوية، 1/3، فنجد أن الوحدة الأصلية قد قسمت إلى 15 جزءا متساويا، 1/15، وعليه يكون 1/3 من الـ 1/5 هو 1/15. وإذا أخذنا اثنين 1/15 من كل من الأخماس الأربعة، نحصل على 2/3 لـ 4/5، أو 8/15.
وكي تضرب كسرين، اضرب بسط الأول في بسط الثاني لتحصل على البسط الجديد، واضرب مقام الأول في مقام الثاني لتحصل على المقام الجديد.
1/2 × 1/4 = (1×1) / (2×4) = 1/8 ، 5/6 × 3/4 = (5×3) / (6×4) = 15/24
وتمثل المساحة ـ الطول × العرض ـ معنى آخر للضرب. وتبلغ المساحة الإجمالية لبطاقة أبعادها 3 سم عرضًا و5 سم طولاً أو 3 في 5، (3×5) سم²، أو 15 سم². ويمكن أيضًا النظر إلى ضرب الكسور على أنه تعبير عن مساحة. فمثلا، يمكن أن يدل 2/3× 4/5 على مساحة مستطيل قياساته 2/3 وحدة في العرض و 4/5 وحدة في الطول. تشتمل المساحة الناتجة من 2/3 وحدة في 4/5 وحدة على ثمانية من الـ 15 جزءًا المتساوية لكامل الوحدة المربعة. وعليه، تكون مساحة المستطيل مساوية 8/15 من مساحة كامل الوحدة المربعة. هذا الجواب هو نفس الجواب الذي وجدناه بوساطة ضرب البسط في البسط وضرب المقام في المقام للكسرين.
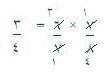
ويمكن في الغالب جعل ضرب الكسور أكثر سهولة وذلك بالقيام أولا بالاختصار. ويتم الاختصار بقسمة كل من البسط والمقام على العدد نفسه، وهو مماثل لقسمة الكسر على واحد، الأمر الذي لا يغير من النتيجة شيئًا. عندما تختصر: اشطب على الحدود القديمة واكتب الحدود الجديدة. وفي المسألة التالية، يمكن اختصار الـ 7، وذلك بقسمة كل من البسط والمقام على 7، ويمكن اختصار الـ 6 والـ 8 بالقسمة على 2:
 |
قسمة الكسور:
يمكن إعادة كتابة مسألة القسمة كمسألة ضرب.63 ÷ 9 تعني ¸كم تسعة توجد في 63 ؟ · أو 9 × ؟ = 63.
9/20 ÷ 3/4 تعنى كم 3/4 يوجد في 9/20؟ أو (3×؟) / (4×؟)= 9/20
يمكن إعادة كتابة السألة الثانية على الشكل:
(9÷3) / (20÷4) = ؟/؟
نرى بمقارنة هذه المسألة مع المسألة الأصلية أنه لتقسيم كسرين، يجب علينا تقسيم البسط على البسط للحصول على البسط الجديد، وتقسيم المقام على المقام للحصول على المقام الجديد.
9/20 ÷ 3/4 = (9÷3) / (20÷4) = 3/5
ومع ذلك، فإن كثيرا من مسائل القسمة لا تصل إلى نتيجة.
2/5 ÷ 3/7 = (2÷3) / (5÷7)
فلا يمكن تقسيم 2 على 3، ولا حتى تقسيم 5 على 7. نستطيع، باستخدام القسمة كمعنى للكسور، إعادة كتابة المسألة الأصلية على شكل كسر مركب. نقول عن كسر أنه كسر مركب إذا كان بسطه كسرًا أو كان مقامه كسرًا أو كان الاثنين معًا.
2/5 ÷ 3/7 = (2/5) / (3/7)
ويمكننا تبسيط هذه المسألة بضرب كسري البسط والمقام في مقلوب المقام. ويعرف مقلوب الكسر بأنه الكسر الناتج عن جعل البسط مقاما والمقام بسطا في الكسر الأصلي. فمقلوب 3/7 هو 7/3. أما حاصل ضرب أي كسر في مقلوبه فيساوي الواحد.
3/7 × 7/3 = (3×7) / (7×3) = 21/21 = 1
وضرب كل من بسط ومقام كسر مركب بمقلوب مقامه هو كمثل ضرب الكسر المركب في واحد. وتنتج هذه العملية كسرًا مكافئًا أكثر بساطة ومقامه واحد.
|
وعليه، 2/5 ÷ 3/7 =2/5 × 7/3، أو 2/5 مضروبا بمقلوب 3/7. ويعادل التقسيم على كسر الضرب بمقلوب الكسر.
2/5 ÷ 3/7 = 2/5 × 7/3 = (2×7) / (5×3) = 14/15
الكسور غير الحقيقية
يسمى الكسر الذي يكون فيه البسط أصغر من المقام كسرًا حقيقيًا. ويسمى الكسر الذي يكون فيه البسط مساويًا للمقام أو أكبر منه كسرا غير حقيقي. وجميع الكسور غير الحقيقية ذات قيمة تساوي أو تزيد على واحد. مثلا، يعبر الكسر 27/20 عن 27 جزءًا من الأجزاء الناتجة من تقسيم وحدة إلى 20 جزءًا متساويا، حيث إن الوحدة الكاملة، تحتوي فقط على 20 من الـ20 جزءا المتساوية، فيجب أن يكون 27/20 أكبر من وحدة واحدة. وهو يزيد عن واحد بـ 7/20.
ويمكن أيضًا كتابة قيمة الكسر غير الحقيقي 27/20 على الشكل 7/20 1. ويطلق على مثل هذا العدد، الذي يجمع عددا صحيحا وكسرا، عددًا مختلطًا، ويساعد التفكير في معنى القسمة للكسور على فهم كيفية تحويل الكسور غير الحقيقية إلى أعداد مختلطة. مثلا، يمكن إعادة كتابة الكسر 26/3 كقسمة 26 على 3.
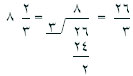 |
لتحويل عدد مختلط إلى كسر غير حقيقي، اكتب أولاً، العدد المختلط على شكل مسألة جمع. مثلاً قيمة العدد المختلط 2/3 5 تساوي 5 + 2/3، أما الخطوة الثانية، فكتابة العدد الصحيح علي شكل كسر. ويمكن كتابة أي عدد صحيح على شكل كسر باستخدام العدد الصحيح كبسط واستخدام الواحد كمقام. وبالتالي يمكن كتابة 5 على الشكل 5/1. أوجد، بعد كتابة العدد الصحيح على شكل كسر، المقام المشترك ثم اجمع:
3/2 5 = 5/1 + 2/3 = (5×3) / (1×3) + 2/3 = 15/3 + 2/3 = 17/3
تتم العملية بصورة مختصرة، بضرب العدد الصحيح بمقام الكسر ثم جمع حاصل الضرب إلى بسط الكسر وكتابة المجموع كبسط جديد. ويبقى المقام ذاته
7/8 6 = [(6×8)+7] / 8 = (48+7)/8 = 55/8
وعند جمع أو طرح أعداد مختلطة يمكن البدء بكتابة الأعداد المختلطة كمسألة جمع. ثم تجمع أو تطرح الأعداد الصحيحة بشكل منفصل عن الكسور.
3/8 9 + 2/5 4 =
|
ومع هذا تظل بعض المسائل التي تتضمن طرح أعداد مختلطة، أكثر تعقيدًا.
1/3 8 - 2/5 4 =
|
|
3 + 14/15 = 14/15 3
ولضرب أو تقسيم أعداد كسرية حوِّلها إلى كسور غير حقيقية. ثم اضرب أو اقسم كالمعتاد.
نبذة تاريخية
قبل أكثر من 4000 سنة مضت، استخدم الفلكيون من قدامى البابليين الكسور الناتجة عن تقسيم وحدة إلى 60 جزءًا، ثم تقسيم كل جزء من هذه الأجزاء إلى 60 جزءًا، وهكذا. ومازال هذا النظام معمولاً به في تحديد الزمن وفي قياس الزوايا بالدقائق والثواني.
وإبان النهضة العلمية في العالم الإسلامي اخترع العلماء العرب والمسلمون طريقة لتسهيل حساب الكسور الستينية. وكان أول من قام بذلك السموءل بن يحيى المغربي (ت 570هـ ، 1175م). فقد عرض السموءل الطريقة الجديدة التي تقوم على النظام العشري في كتابه القوامي في الحساب الهندي. ثم جاء من بعده غياث الدين الكاشي فطوّر طريقة السموءل في كتابه مفتاح الحساب. وقد ذكر أنه هو الذي اخترع الكسور ليسهل الحساب للأشخاص الذين يجهلون الطريقة الستينية.
واستخدم علماء الرياضيات المصريون الذين ساعدوا في بناء الأهرامات قبل أكثر من 4000 سنة مضت الكسور التي فيها البسط 1 فقط. وتسمى مثل هذه الكسور كسور وحدة. وقد أدى الاقتصار على استخدام كسور الوحدة فقط، إلى ضرورة التعبير عن الأجزاء الكسرية الأخرى على شكل مجاميع. مثلا يعبر عن ¾ بدلالة كسور الوحدة على الشكل ½ + ¼.
وقبل 2,000 سنة كتب الإغريق القدامى عن الكسور بشكل يكون فيه البسط في الأسفل والمقام في الأعلى، ولم يفرقوا بين البسط والمقام بخط. وقد بدأوا فيما بعد، بكتابة الكسور بشكل يكون فيه البسط في الأعلى، والمقام في الأسفل. وقد أخذ علماء الرياضيات الهنود هذه الطريقة في كتابة الكسور من اليونانيين القدامى.
وخلال القرن الثامن الميلادي فتح العرب أجزاء من الهند وتعلموا هناك النظام العشري وهذه الطريقة في كتابة الكسور. وقد نشر العرب، خلال 300 سنة أعقبت ذلك، هذه المعلومات في غربي آسيا وشمالي إفريقيا وأسبانيا. ونشرت خلال أواخر القرن الخامس عشر الميلادي، في أوروبا عدة كتب في الحساب شرحت استخدام الكسور والنظام العشري. وبعد نشر هذه الكتب، بدأ عدد كبير من الأوروبيين في استخدام الكسور في إنجاز العمليات الحسابية اليومية.
تستخدم الكسور اليوم على الأكثر في التعامل مع الإنشاءات والأكواب والأرطال ومقاييس أخرى في نظام القياسات الإنجليزي. ومع هذا، تستخدم معظم البلدان عدا الولايات المتحدة النظام العشري في الأوزان والمقاييس. ويستخدم النظام المتري للقياسات الكسور العشرية والتي تكتب باستعمال الفاصلة العشرية أكثر من استعمال البسط والمقام. ★ تَصَفح: النظام المتري.
وكذلك فإن العديد من المسائل التي كانت تحل عن طريق الكسور وباستخدام الورقة والقلم، وأصبحت تحل باستخدام الحاسبات الإلكترونية التي تعبر عن الكسور بالنظام العشري. ونظرًا لهذه التغيرات فإن استخدامات الكسور تقل يومًا بعد يوم. ومع هذا تظل الصيغة الكسرية أداة مهمة للتعبير عن المعدلات والنسب والقسمة، كما تظل ذات أهمية في الجبر وفي بعض فروع الرياضيات الخاصة كطريقة لكتابة الأعداد النسبية.
تماريـــن
1 - يقوم بيت هند على رقعة من الأرض مساحتها ربع هكتار. اشترى والدها رقعة أرض مجاورة مساحتها ثلاثة أثمان الهكتار. ما مساحة رقعتي الأرض معًا ؟
2 - تستعمل ليلى ¼ ملعقة من القهوة في إعداد كوب واحد من القهوة. كم ملعقة من القهوة يجب أن تستعمل في إعداد ستة أكواب من القهوة ؟
3 - يستطيع بدر قياس المسافات بالخطى. ويبلغ متوسط طول خطوته ¾م. وتبلغ غرفته 7 خطوات طولاً و6 خطوات عرضًا. فكم طول غرفته؟ وكم عرضها بالأمتار؟
أجوبة التمارين
(1) 5/8 هكتار.
(2) 1/2 1 ملعقة
(3) 1/4 5م، 1/2 4م.