القسمة ( Division )
☰ جدول المحتويات
القـِسْـمـة طريقة لفصل أوتجزئة مجموعة أشياء إلى أجزاء متساوية. افترض أن لديك 18 كرة وترغب في قسمتها بالتساوي مع صديقين لك. لمعرفة كم كرة يمكن أن ينالها كل واحد، يمكنك توزيع الكرات إلى ثلاث مجموعات متساوية في كل منها ست كرات كما هو موضح بالشكل.
 |
القسمة واحدة من العمليات الأساسية الأربع في الحساب. أما العلميات الأخرى فهي الجمع والطرح والضرب. وقبل البدء بتعلم القسمة عليك أن تتعلم كيف تجمع وتطرح وتضرب.
| مصطلحات القسمة | ||||||||||||||
|
تعلم القسمة
 |
عملية القسمة تقيس قدرات الطالب الحسابية. |
كتابة القسمة:
إحدى الطرق في تجزئة مجموعة إلى أجزاء متساوية هي في وضعها بأسلوب العد على شكل أجزاء متساوية. لكن هناك طريقة أكثر سهولة للقسمة ؛ مثلا لإيجاد عدد المجموعات التي تتكون من 3 وحدات في الرقم 12، يمكنك مواصلة طرح 3 من 12 حتى لايبقى شيء.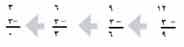 |
يرمز لكل عملية أساسية في الحساب برمز خاص. ورمز القسمة هو ÷ تعني العبارة 12 ÷ 3 = 4. أي أنه عندما نوزع 12 شيئا إلى مجموعات كل منها مؤلفة من ثلاثة أشياء نحصل على أربع مجموعات. أو أنه يوجد أربع ثلاثات في 12. أيضا، يمكن أن تعني أنه إذا وزع 12 شيئا إلى ثلاث مجموعات فيوجد أربعة أشياء في كل مجموعة. عادة، يقرأ الإنسان العارف بالقسمة 12 ÷ 3= 4 على النحو 12 تقسيم 3 يساوي 4. ويمكن أيضا كتابة مسألة القسمة على الشكل:
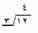 |
ويطلق على أجزاء أو مكونات القسمة أسماء خاصة هي: المقسوم، هو العدد المطلوب تقسيمه.
والمقسوم عليه هو العدد الذي نقسم عليه. وخارج القسمة هو نتيجة القسمة.
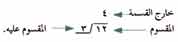 |
طريقة أخرى لكتابة المسألة في القسمة هو الشكل المستخدم في كتابة الكسور. ★ تَصَفح: الكسر.
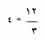 |
مُسلّمات (حقائق) القسمة:
لقد اكتشفت باستخدامك الطرح أنه يوجد في 12 ثلاث مجموعات في كل منها 4 أشياء، أو 12 ÷ 3 = 4. نطلق على هذه حقيقة أو مسلمة قسمة.يمكنك باستخدام الطرح إيجاد جميع مسلمات القسمة (يمكن تسميتها جدول القسمة)، أو مسلمات القسمة الـ64
ومن المهم أن تتعلم جدول القسمة بشكل جيد كي تستطيع استخدامه مباشرة. هذه المسلمات نفسها مفيدة، وهي أيضا ضرورية لتعلم كيفية تقسيم أعداد أكبر بسرعة وبدقة.
 |
القسمة المطولة
هي طريقة يمكن استخدامها لتقسيم أعداد كبيرة. ويتعين عند استخدامها تدوين أو تسجيل الخطوات بدقة.
لنفترض أنك تريد إيجاد كم ثلاثة في 79، أو 79 ÷ 3 بدلا من طرح 3 واحدة في كل مرة، يمكن اختصار العمل بطرح عدة ثلاثات دفعة واحدة. يمكنك، كبداية، طرح خمس ثلاثات، أو 15، في كل مرة.
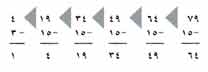 |
ويكون كجملة قد طرحت 5 + 5 + 5 + 5 + 5 أو خمسًا وعشرين ثلاثة من 79، مبقيًا على 4، لايمكن طرح خمس ثلاثات أخرى، ولكن يمكنك طرح 3 واحدة تاركًا باقيًا 1. وعليه، يوجد 25 + 1 أو ست وعشرون ثلاثة في 79 مع بقاء 1 زيادة.
لقد اختصرت العمل بطرحك 5 ثلاثات في كل مرة. يمكن بعدها محاولة طرح عشرة ثلاثات، أو 30، كل مرة:
 |
تكون، هذه المرة، قد طرحت 10 + 10 + 5 +1 أو ستًا وعشرين ثلاثة من 79، وتركت باقيا 1. ويكون الأسلوب أو الشكل التالي هو المستحسن في الأداء.
 |
يمكنك بعد شيء من التمرين أن تطرح عشرين ثلاثة ثم ست ثلاثات.
 |
كي تكتسب مزيدا من الخبرة في القسمة المطولة يمكنك الآن محاولة معرفة كم 21 يوجد في 891، أو 891÷ 21. عليك أولا، أن تقرر كم 21 سوف تطرح دفعة واحدة. إن عشرة 21، أو 210، يمكن أن تثبت صلاحيتها. إن استعمال العشرات أو المئات أو الألوف في ضرب المقسوم عليه يجعل القسمة أكثر سهولة.
 |
عندما طرحت أربعة 210 أو أربعين 21، وجدت أن الباقي، 51، صغير جدا لتطرح منه عشرة 21 إضافية، يمكنك، على كل حال، طرح 21 واحدة كل مرة يعطيك هذا أخيرا 10 + 10 +10 + 10 + 1 + 1 أو اثنين وأربعين 21 في 891 مع باق 9.
كان باستطاعتك استخدام عشرين 21، أو 420،
 |
والمثال التالي الأخير سوف يوضح بصورة أكبر عملية القسمة المطولة. افترض أنك ترغب في معرفة كم 37 يوجد في 12,526 أو 12,526 ÷ 37، عليك، مرة أخرى، أن تقرر كم 37 ستطرح دفعة واحدة.
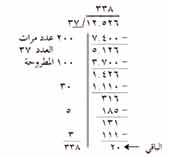 |
يمكن أن تجرب على ورقة مسودة لتجد الوحدات التي يمكن استعمالها لحل المسألة بسهولة. حتى إأنك تستطيع استعمال وحدات تزيد عن 200
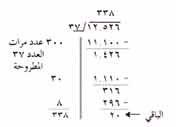 |
يستخدم أشخاص كثيرون طريقة للقسمة المطولة أكثر اختصاراً من تلك التي شرحناها فيما سبق. ويبدو هذا واضحًا في الخطوات الثلاث التالية:
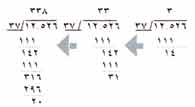 |
تؤدي هذه الطريقة إلى نفس النتائج التي ناقشناها فيما سبق ولكن بأسلوب مختلف. وهي لاتوضح عملية القسمة بجلاء للمبتدئين. وعند استخدام هذه الطريقة المختصرة يكون من المفيد في جمــيع هذه الأمثلة ملاحـــظة كتــابة الناتج في الخانات المناسبة أعــلى المقسوم. أي عندما تطـــرح عددا من مضــاعفات الـ 100، لابد أن تسجل هذا العدد أعلى منزلة المئات للمقسوم.
باقي القسمة:
يوجد في الغالب باق عندما تستكمل مسألة في القسمة.ويعتمد تصرفك في هذا الباقي على نوع المسألة، فإذا كنت ترغب في معرفة كم ثلاثة توجد في 79. وكانت لديك 79 قرشاً تريد صرفها على طوابع بريدية قيمة كل منها 3 قروش، سوف تجد أنه بإمكانك شراء 26 طابعاً ويبقى لديك قرش واحد.إذا أردت توزيع 79 تفاحة بين ثلاثة أشخاص، سوف تجد أيضا أنه يوجد ست وعشرون 3 في 79 ويبقى 1 هذا يعني أن كل شخص يحصل على 26 تفاحة وتبقى تفاحة واحدة مشتركة. وإذا كان لابد من تساوي الحصص تماماً، فعليك قطع التفاحة الباقية إلى ثلاثة أجزاء متساوية. وسوف يحصل كل شخص على 1/3 26 تفاحة.
توضح هذه الأمثلة أن ما نصنعه في الباقي يعتمد على المسألة. وفي بعض الحالات يشار إلى مزيد من التقسيم لأجزاء كسرية. وفي حالات أخرى يكون الباقي مجرد إعلام عن الكمية المتبقية.
قسمة الكسور العشرية:
يمكنك أيضا استخدام القسمة المطوَّلة في تقسيم أعداد تحتوي على كسور عشرية. العبارة 78,35 ÷ 3,6 هي مسألة من هذا النوع. عليك، كي تفهم قسمة الكسور العشرية، أن تتعلم خاصية مهمة للقسمة. تعلم أن 15 ÷ 3 = 5 هي حقيقة أو مسلمة قسمة. ماذا يحدث لو ضربت الـ 15 والـ 3 بـ10؟. يعني، ما النتيجة في قسمة 150 على 30؟ سيتضح بقسمة مطولة أن الحاصل هو 5 أيضا. وهكذا، فإن 15 ÷ 3 = 5 و150 ÷ 30 = 5. بشكل مشابه، 72 ÷ 6 = 12 و720 ÷ 60= 12. إذا ضربنا الـ 72 والـ 6 في 100 فسيكون الحاصل في 7200 ÷ 600 هو 12 أيضًا.توضح هذه الأمثلة القاعدة العامة التالية :
إذا ضُرب كل من المقسوم والمقسوم عليه في 10 أو 100 أو1000 أو عدد مخالف للصفر لايتغير حاصل القسمة.
يمكن استخدام هذه القاعدة لتقسيم 78,35 على 3,6. يمكن ضرب كل من 78,35 و 3,6 في10. وعليه، 78,35 × 10 = 783,5 و 3,6 × 10 = 36. وسيكون الناتج في 783,5 ÷ 36 نفس الناتج في 78,35÷ 3,6. غير أن الفواصل العشرية أخذت الآن مواضع جديدة.
القسمة المختصرة
يمكنك في حالة التقسيم على عدد من رقم واحد مثل 7، القيام بالعمل دون تدوينه وتسمى مثل هذه القسمة قسمة مختصرة وينجز فيها العمل، عادة، في الذهن أكثر مما هو على الورقة. وهي نفس الطريقة المتبعة في القسمة المطولة غير أن العمل فيها يتم ذهنيا.
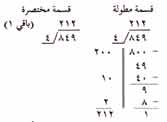 |
الاختلاف الوحيد بين هذين المثالين هو أنه في القسمة المختصرة يتم العمل ذهنيا ويشار للباقي إلى جانب الناتج. سوف نستخدم الحرف ب للدلالة على الباقي. أول ماترى في هذا المثال هو أن بإمكانك طرح مائتي 4 من 849. اكتب 2 في خانة المائة أعلى الـ 8 في المقسوم، بعدها، يمكنك طرح عشر أربعات من الـ 49 الباقية. أكتب 1 في منزلة العشرات أعلى الـ 4 في المقسوم. أخيرا يمكن طرح أربعتين من الـ 9 الباقية. اكتب 2 في منزلة الآحاد فوق الـ 9 في المقسوم. اكتب الباقي إلى يسار الحاصل.
وفي المسائل الأكثر صعوبة في القسمة المختصرة يجب استخدام وسيلة جديـدة وهذا ما سيتضـح في المسألــة 415 ÷ 7.
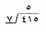 |
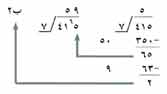
فأول خطوة في حل هذه المسألة هو أن تطرح خمسين 7 أو 350 والتي هي خمس وثلاثون 10. اكتب 5 لأجل 50 أو خمس عشرات أعلى الـ 1 في المقسوم. ثم بعملية الطرح ذهنيا. إن حاصل طرح خمس وثلاثين 10 من إحدى وأربعين 10 هو ست عشرات. اكتب 6 صغيرة إلى يسار العدد 5 في المقسوم.
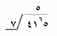 |
اقسم الآن ست عشرات وخمسة، أو 65 على 7. تستطيع طرح تسع سبعات أو 63 من 65، تاركًا باقيًا.
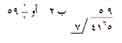 |
ومن المفيد معرفة كيف انشقت هذه العملية من القسمة المطولة:
 |
ومثال آخر هو 7536 ÷ 9، وكما في حالة القسمة المطولة، يجب أن تقرر كم 9 تطرح في وقت واحد.
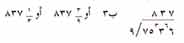 |
تطرح أولا ثمانمائة 9، أو 7200، اكتب 8 لأجل ثمانمائة أو 800 أعلى الـ 5 في المقسوم. اطرح ذهنيا 72، مائة من 75، مائة : 75 - 72 = 3. اكتب 3 صغيرة إلى يسار الـ3 في المقسوم لإبقاء الثلاث 100 مشمولة في العمل. تطرح ثلاثين 9 أو 270 من العدد 336 الجديد. اكتب 3 لأجل ثلاثين 9 أعلى الـ 3 في المقسوم. بعدها 33 - 27= 6. اكتب 6 صغيرة إلى يسار الـ 6 في المقسوم لإبقاء الست عشرات مشمولة في العمل. يمكنك طرح سبع تسعات، أو 63 من العدد الجديد 66. اكتب 7 لأجل سبع تسعات أعلى الـ 6 في المقسوم. أخيرًا 66 - 63 = 3. وضح الباقي بكتابته إلى يسار الحاصل.
سيكون باستطاعتك، بعد شيء من التمرين، التخلي عن الأرقام الصغيرة كرموز تذكرك بالمقادير التي يجب أن يشملها العمل. وستكون قريبًا قادرًا على أن تتذكِّر هذه الأعداد في ذهنك.
التحقق من نتيجة القسمة
سيكون من الحكمة التحقق من الجواب لمسألة قسمة لتكون متأكدًا من صحة حلك.
التدوير:
أحد طرق التحقق هو أن ترى إن كان الجواب معقولاً أم لا. يمكنك تقدير أو تخمين الحاصل عن طريق تدوير ؛ أي تقريب المقسوم والمقسوم عليه. لتخمين الحاصل في 158 ÷ 76، تستطيع تدوير أو تقريب العدد 158 إلى 160 والعدد 76 إلى 80. لكون 160 ÷ 80 = 2 فإن الحاصل في 158 ÷ 76 يجب أن يكون حوالي 2. لتخمين الحاصل في 5124 ÷ 36، يمكنك تدوير 5124 إلى 5000 و36 إلى 50. من الواضح أن 5000 - 50 = 100 و 5000 ÷ 25 = 200 وعليـه، يجـب أن يكون الحاصل في 5124 ÷ 36 مابين 100 و 200. سيساعدك تخمين الجواب في تقرير ما إذا كان جوابك منطقيًا.التحقق باستخدام الضرب:
طريقة أخرى للتحقق من الحاصل هي ضرب الحاصل بالمقسوم عليه ورؤية إن كان الناتج يساوي المقسوم. إذا كان ضربك صحيحا فتكتشف بهذه الطريقة أي خطأ. ذلك لأن الضرب عكس القسمة.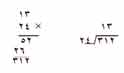 |
يوضح المثال التالي كيف يستعمل الباقي عند التحقق بوساطة الضرب :
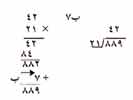 |
يضرب الحاصل بالمقسوم عليه ويضاف الباقي إلى الناتج.
أربع أفكار أساسية في القسمة
إليك أربع قواعد مهمة عليك أن تتذكرها في حل مسائل القسمة :
1- تذكر أن القسمة هي تجزئة عدد أو مجموعة إلى مجموعات أصغر متساوية. يمكن للمقسوم عليه أيضا إيضاح حجم هذه المجموعات أو عددها.
2- تعلم جدول القسمة أو مسلمات القسمة بشكل جيد، بحيث لاتحتاج للتوقف في كل مرة لاستنتاجها، ستستخدمها باستمرار في الحسابات اليومية، وسوف تحتاج معرفتها عند قسمة أعداد كبيرة.
3- تذكر الطريقة المتبعة في القسمة المطولة لتقسيم الأعداد الكبيرة. اطرح من المقسوم أكبر عدد ممكن من المرات من المقسوم عليه في الخطوة الواحدة. تستطيع بهذا الشكل اختصار عدد الخطوات في إجراء القسمة المطولة.
4- تحقق دومًا من الجواب بعد انتهاء مسألة القسمة. تستطيع ذلك، إما بطريقة التخمين أو بطريقة ضرب الحاصل في المقسوم عليه وإضافة الباقي، إن وجد.
تمارين على القسمة
 |
16 - يعتزم فصل السيدة ليلى في المدرسة القيام بزيارة لمقر جريدة محلية. عرضت بعض الأمهات سياراتهن لنقل الأطفال. يوجد 35 طفلا في الفصل، وتتسع كل سيارة لـخمسة أطفال. كم سيارة تحتاج هذه الرحلة؟
17 - يوجد 7 أيام في الأسبوع. كم أسبوعًا يوجد في سنة واحدة (في 365 يوما)؟
18 - ثمن قطعة شوكولاتة 13 قرشا. كم عدد قطع الشوكولاتة التي تستطيع سوزان شراءها بـ 91 قرشا؟
19 - يريد 4 أولاد تقاسم 64 قطعة شوكولاتة، كم قطعة سيكون نصيب كل ولد؟
20 -يقود أحمد دراجته بسرعة 6 كم الساعة. كم ساعة تستغرق منه قطع مسافة 15 كم؟
21 - تطير طائرة بسرعة مقدارها 560 كم/ الساعة. ما الزمن اللازم كي تطير مسافة 1,260 كم؟
22 - قام سعود ووالده برحلة بالسيارة. قطعا 613,9كم خلال 10 ساعات و 18 دقيقة. كم كان معدل سرعة السيارة؟
23 - استاجر والد مريم شقة بـ 2520 جنيها في السنة، كم يجب أن يدفع إيجارًا لشهر واحد؟
أجوبة تمارين القسمة
|