المثلث هو أحد الاشكال الاساسية في الهندسة.و هو شكل ثنائي الأبعاد مكون من ثلاثة رؤوس تصل بينها ثلاثة اضلاع، التي هي عبارة عن قطع مستقيمة.
فهرس |
أنواع المثلثات
من الممكن تصنيف المثلثات تبعا لاطوال اضلاعها كما يلي:
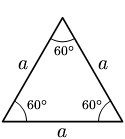
- مثلث متساوي الأضلاع: هو مثلث أضلاعه متساوية. جميع زوايا المثلث متساوي الاضلاع متساوية أيضا، وقيمتها 60 درجة.
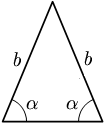
- مثلث متساوي الضلعين: هو مثلث فيه ضلعان متساويان. الزاويتان المقابلتان لهذين الضلعين تكونان متساويتان أيضا.
- مثلث مختلف الأضلاع: هو مثلث أطوال أضلاعه مختلفة. زوايا هذا المثلث تكون مختلفة القيم أيضا.
.
كما يمكن تصنيف المثلثات تبعا لقياس أكبر زاوية في المثلث:
- مثلث قائم: له زاوية قياسها 90 درجة (زاوية قائمة)، يدعى الضلع المقابل للزاوية القائمة بالوتر، وهو أطول أضلاع هذا المثلث.
- مثلث منفرج الزاوية: له زاوية قياسها أكبر من 90 درجة واصغر من 180 درجة(زاوية منفرجه)
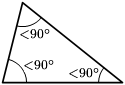
- مثلث حاد الزوايا: كل زواياه قياسها أصغر من 90 درجة (زاوية حادة).
| صورة:Triangle.Right.png | 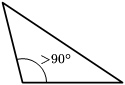 |
 |
| قائم | منفرج | حاد |
حقائق عن المثلثات
| صورة:Triangle.Labels.png |
| مثلث مع رموز عناصره |
تشابه مثلثين
يقال عن مثلثين انهما متشابهين اذا كانت الزوايا المتقابلة من كل منهما متساوية، اي عندما ينتج احدهما عن الاخر بتكبيره او تصغيره. ان اطوال اضلاع المثلثين المتشابهين متناسبة، اي انه اذا كان طول اقصر اضلاع المثلث الاول هو ضعفا طول اقصر اضلاع المثلث الثاني، فان طول كل من الضلعين الاطول و المتوسط من المثلث الاول هو ضعفا طولي لضلعين الاطول و المتوسط من المثلث الثاني ايضا، و بالتالي فان النسبة بين طولي الضلعين الاقصر و الاطول في المثلث الاول مساوية للنسبة بين طولي الضلعين الاقصر و الاطول في المثلث الثاني.وهناك عدة حالات للتشابه منها زاوتين ويرمز للتشابه بالرمز (~) يتشابه مثلثان اذا تطابقتزواياهما المتناظرة ___ اذا تطابقت زاويتان في مثلث مع زاويتان في مثلث اخر كان المثلثان متشابهين.
نظرية فيثاغورث
واحدة من النظريات الاساسية في المثلثات هي نظرية فيثاغورث و التي تنص على انه في المثلث القائم، مربع طول الوتر (ا َ) يساوي إلى مجموع مربعي طولي الضلعين القائمين (ب َ، ج َ)، اي:
د َ² = ب َ² + ج َ²
مما يعني ان معرفة طولي ضلعين من المثلث القائم، كاف لمعرفة طول الضلع الثالث:
من الممكن تعميم نظرية فيثاغورث لتشمل اي مثلث عبر قانون التجيب:
د َ² = ب َ² + ج َ² - 2 ب َ ج َ تجب د
و هو صحيح من اجل كل المثلثات حتى و لو لم تكن د قائمة.
سؤال:هل تبقى النظرية صحيحة في حالة ان تكون الاشكال المقامة مضلعات منتظمة اخرى مثل مضلع ثلاثي:أو خماسي أو سداسي،...الخ ماهو تعريف علم المثلثات
خطأ رياضيات (خطأ في الصيغة): أدخل الصيغة هنا ===مساحة المثلث===
تعطى مساحة المثلث بالقوتلةنتالتالابانون:
سط = ق × ع / 2
حيث ان ق هي طول احدى اضلاع المثلث (القاعدة)، و ع هو طول العمود النازل على هذا الضلع من الرأس المقابل له (الارتفاع).
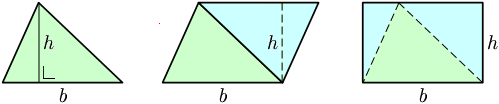
من الممكن البرهان على ذلك من خلال الشكل التالي:
مثلث أحد الأشكالِ الأساسيةِ في هندسة: شكل ثنائي الأبعاد بثلاثة قِمَم وثلاثة جوانبِ بشكل خطوط مستقيمة . عرف المثلثات
أنواع المثلثاتِ
المثلثات يُمْكِنُ أَنْ تُصنّفَ طبقاً للأطوالِ النسبيةِ مِنْ جوانبِها:
- في مثلث متساوي الأضلاع كُلّ الجوانب ذات طولِ متساو. مثلث متساوي الأضلاع أيضاً متساوي الزوايا ، أي أن كل زاوية هي 60 درجة؛ * في مثلث متطابق الضلعين جانبان متساويان في الطول. مثلث متساوي الساقين لَهُ زاويتان داخليتانُ متساويتانُ أيضاً.
- في مثلث مختلف الأضلاع كُلّ الجوانب لَها أطوالُ مختلفةُ. إنّ الزوايا الداخليةَ في مثلث مختلف الزوايا هي مختلفة أيضا.
المثلثات يُمْكِنُ أيضاً أَنْ تُصنّفَ طبقاً لحجمِ زاويتِهم الداخليةِ الأكبرِ، وَصفَ تحت استعمال درجة مِنْ القوسِ.
- أي مثلث قائم (أَو مثلث قائم الزاوية ) عِنْدَهُ 90 واحد °؛ الزاوية الداخلية (a زاوية قائمة). الجانب قبالة الزاوية القائمة وتر زاوية قائمة ؛ هو الجانبُ الأطولُ في المثلث القائمِ. إنّ الجانبانَ الآخرَ سيقان المثلثِ.
- مثلث منفرج عِنْدَهُ زاويةُ داخليةُ واحدة أكبرُ مِنْ 90 °؛ ( زاوية منفرجة).
- مثلث حادّ عِنْدَهُ زوايا داخليةُ التي جميعاً أصغر مِنْ 90 °؛ (ثلاثة زاوية حادة ).
نقاط و مستقيمات و دوائر متصلة بالمثلث
- الموسط العمودي لمثلث هو مستقيم يمر من أحد اضلاع المثلث في منتصفه و يكون عموديّا عليه و تتلاقى الوسطات العمودية لمثلث في نقطة تسمى مركز الدائرة المحيطة بمثلث و يكون لهذه النقطة نفس البعد عن رؤوس المثلث الثلاث و يكون تقاطع موسطين عموديين فقط كافيا لمعرفة مركز هذه الدائرة.
- تقول مبرهنة طالس انّه اذا مركز الدائرة المحيطة بالمثلث توجد على ضلع من أضلاع المثلث فانّ الزاوية المقابلة لهذا الضلع تكون قائمة.
.
- الارتفاع هو قطعة مستقيم تكون صادرة من راّس من رؤوس المثلث و تكون عمودية غلى الضلع المقابل و يمثل الارتفاع البعد بين الراس و الضلغ المقابل كما تتقاطع الارتفاعات في نقطة تسمى المركز القائم.
.
- منصف الزاوية هو مستقيم يمرّ من راس من رؤوس المثلث و يقسم الزاوية إلى نصفين و تتقاطع المنصفات الثلاثة في مركز الدائرة المحاطة بالمثلث وهي الدائرة التي تمسّ اضلاع المثلث الثلاث.
- الموسّط هو قطعة مستقيم تنطلق من رأس من رؤوس المثلث و تمر من منتصف الضلع المقابل و تتقاطع الموسطات الثلاث في نقطة تسمى مركز ثقل المثلث و يكون تقاطع موسطين فقط كافيا لمعرفة مركز الثقل. كما يكون البعد بين راس المثلث و مركز الثقل مساويا ل 2/3 الموسط الصادر من ذلك الراس.
- منتصفات الاضلاع الثلاث و نقطة تقاطع الارتفاع و الضلع المقابل له موجودة كلها على نفس المثلث دائرة النقاط التسع للمثلث و النقاط الثلاثة المتبقية هي منتصف البعد بين راس المثلث والمركز القائم و شعاع دائرة النقاط التسع هي نصف شعاع الدائرة المحيطة بالمثلث .
حساب مساحة المثث
أبسط طريقة لحسا مساحة المثلث و أكثرها شهرة هي
حيث S هي المساحة و bهي طول قاعدة المثلث و hهو ارتفاع المثلث . قاعدة المثلث تمثل ايّ ضلع من أضلاع المثلث و الارتفاع هو المستقيم الصادر من الراس المقابل للضلع و العموديّ عليه.
اقرأ ايضا
وصلات خارجية
- Triangle Calculator - solves for remaining sides and angles when given three sides or angles, supports degrees and radians.
- Clark Kimberling: Encyclopedia of triangle centers. Lists some 3200 interesting points associated with any triangle.
- Christian Obrecht: Eukleides. Software package for creating illustrations of facts about triangles and other theorems in Euclidean geometry.
- Proof that the sum of the angles in a triangle is 180 degrees
- Area of a triangle - 7 different ways
- Triangle definition pages with interactive applets that are also useful in a classroom setting.
- Animated demonstrations of triangle constructions using compass and straightedge.
- Triangles: Theorems and Problems. Interactive illustrations at Geometry from the Land of the Incas.
- Many things about triangles
- Triangle in light aircraft
- All Math Words Encyclopedia for grades 7-10.