مبرهنة الكاشي

شكل. 1 - المفاهيم المستعملة في مثلث ما.

مبرهنة الكاشي خاصة بهندسة المثلثات و هي تعميم لمبرهنة فيتاغورس في المثلثات التي ليست لها زاوية قائمة: و هي تربط الضلع الثالث لمثلث بالضلعين الآخرين و جيب تمام الزاوية المكونة لهما.

نعتبر مثلث ABC, حيث نستعمل المفاهيم الموجودة في الشكل1: من جهة α, β و γ بالنسبة للزوايا, و من جهة أخرى a, b و c بالنسبة للأضلاع. مبرهنة الكاشي هي:

$\,c^2=a^2+b^2-2ab\cos\gamma$ .

فهرس

// تاريخ
// تطبيقات
// البرهنة
- بتقسيم المساحات
- باستعمال نظرية فيتاغورس

تاريخ

شكل. 2 - مثلث ABC مع ارتفاع BH

في كتاب العناصر لإقليدس, نجد مقاربة هندسية لتعميم مبرهنة فيتاغورس: نجد في الكتاب2 العبارتين 12 و 13, حيث يتم التطرق لحالة مثلث عادي بزاوية منفرجة و في مثلث عادي بزوايا حادة. لكن عدم وجود الدوال المثلثية (آنذاك) و كذلك الجبر أدى إلى استعمال المساحات.

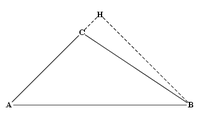
فالعبارة 12 : مربع الضلع الذي يحمل الزاوية المنفرجة أكبر من مربعي الضلعين الآخرين: و باستعمال المثلث ABC بزاوية منفرجة في A و ارتفاع H (شكل2) الصيغة تصبح: AB² = CA² + CB² + 2 CA CH.

و كان يجب انتظار العرب المسلمين لتظهر الدوال المثلثية لرؤية المبرهنة في تطورها: فالفلكي و الرياضي البتاني عمم نتيجة إقليدس في الهندسة الفضائية و التي مكنت من القيام بحساب المسافات بين النجوم. و في نفس الوقت تم إنشاء جداول للدوال المثلثية و التي أتاحت للكاشي صياغة المبرهنة في شكلها النهائي.

تطبيقات

مبرهنة الكاشي في تعميم لمبرهنة فيتاغورس, عندما تكون الزاوية :

$γ$ قائمة, أو عندما يكون: $cosγ = 0$ , المبرهنة تصبح: $\,c^2=a^2+b^2$ ,

و عكسيا.

شكل. 3 - تطبيق المبرهنة :الكاشي زاوية أو ضلع مجهول.

النظرية تستعمل في المثلثات(انظر شكل. 3)حل مثلث,أي تحديد:

الضلع الثالث لمثلث نعرف فيه زاوية و الضلعين المكونين لها:

$\,c = \sqrt{a^2+b^2-2ab\cos\gamma}$ ;

زوايا مثلث نعرف فيه الأضلاع:

$\,\gamma = \arccos \frac{a^2+b^2-c^2}{2ab}$ .

البرهنة

بتقسيم المساحات

من بين طرق البرهنة حساب المساحات، حيث يتم ملاحظة ما يلي:

$a 2$ , $b 2$ و $c 2$ هي مساحات لمربع أضلاعه على التوالي $a$ , $b$ و $c$
$a b | cosγ |$ و هو ل متوازي أضلاع من جهة $a$ و $b$ يكونان زاوية $π / 2 - γ$ , تغيير إشارة: $cosγ$ تصبح الزاوية $γ$ منفرجة تجعل دراسة الحالات ضرورية.

شكل. 4أ - البرهنة بالنسبة للزوايا الحادة : « طريقة التقسيم ».

الشكل 4أ (جانبه) يقسم سباعي بكيفيتين مختلفتين حيث تتم البرهنة في حالة زاوية حادة. يدخل هنا :

بالوردي, lالمساحات $a 2$ , $b 2$ في اليسار, و المساحات $2 a b cosγ$ و $c 2$ في اليمين ;
بالأزرق, المثلث ABC, في اليمين كما في اليسار ;
بالرمادي, بعض المثلثات الإضافية, متطابقة مع المثلث ABC و بنفس العدد في التقسيمين.

تساوي المساحات في اليمين و اليسار يعطي

$\,a^2+b^2 = c^2+2ab \cos\gamma$ .

شكل. 4ب - البرهنة بالنسبة للزوايا المنفرجة : « طريقة التقسيم ».

الشكل 4ب (جانبه) يقسم سداسي بكيفيتين مختلفتين بكيفية برهن في حالة زاوية منفرجة. الشكل يبين

بالوردي, المساحات $a 2$ , $b 2$ و $- 2 a b cosγ$ في اليسار, و المساحات $c 2$ في اليمين ;
بالأزرق, مرتين المثلث ABC, في اليمين كما في اليسار.

تساوي المساحتين يمينا و يسارا يعطي

$\,a^2+b^2-2ab\cos\gamma = c^2$ .

باستعمال نظرية فيتاغورس

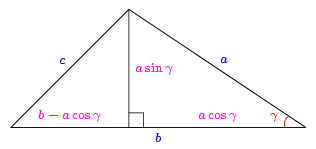
شكل. 5 - البرهنة باستعمال العلاقات المثلثية

الشكل 5 (جانبه) يبين طريقة البرهنة باستعمال مبرهنة فيتاغورس في مثلث قائم الزاوية ناتج عن طريق الارتفاع : $\,c^2 = (a\sin\gamma)^2 + (b-a\cos\gamma)^2$

بنفس الطريقة نبرهن في حالة مثلث بزاوية منفرجة

تصنيفات الصفحة: مبرهنات رياضية | مقالات مختارة في fr