التباديل والتوافيق ( Permutations and Combinations )
☰ جدول المحتويات
التباديل والتوافيق أسماء يعبر بها علماء الرياضيات عن مجموعات معينة من الأشياء أو الرموز. والتباديل ترتيبات منظمة لمجموعة من الأشياء، فمثلاً تعد (أ ب جـ) و(أ جـ ب) و(ب أ جـ)، ثلاثة تباديل لمجموعة الرموز أ، ب، جـ. أما التوافيق فهي تلك المجموعات التي تتضمن الأشياء نفسها بغض النظر عن الترتيب، فالمجموعات (أ ب جـ) و(أ جـ ب) و(ب أ جـ) كلها تمثل التوافيق نفسها، بينما تمثل المجموعات (أ ب جـ) و(أ ب د) و(أ جـ د)، توافيق مختلفة.
يطلق مسمى توافقيات على ذلك الفرع من الرياضيات الذي يتناول التباديل والتوافيق. وللتباديل استخدامات عديدة تشمل تحويل المكالمات الهاتفية عبر الأسلاك، وجدولة الإنتاج فى المصانع. ومع استخدام الحاسوب، غدت التباديل مجالاً خصبًا للأبحاث، وذلك لسرعة الحاسوب في القيام بالحسابات المتكررة.
حساب التباديل
سؤالنا عن ¸عدد مجموعات الأحرف التي يمكن تشكيلها من الأحرف الثلاثة أ ، ب، جـ· هو سؤالنا نفسه عن عدد التباديل الممكنة لثلاثة أشياء يؤخذ 3 منها في كل مرة. وبالإمكان الإجابة عن هذا السؤال عن طريق 1- حصر كل الاحتمالات الممكنة 2-التفكير الاستنتاجي 3- استخدام الصيغ الرياضية.
طريقة الحصر:
كل ما تحتاجه لإيجاد الجواب هنا هو كتابة كل الاحتمالات الممكنة ومن ثم عدها. وتوضح القائمة أدناه وجود ستة احتمالات، وبالتالي فهناك 6 تباديل لثلاثة أشياء تؤخذ 3 منها في كل مرة.
|
ويمكن أيضًا حصر الاحتمالات الممكنة على هيئة رسم تفرعي غير مقفل يبين خيارات كل خانة.
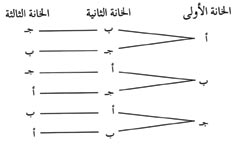 |
ويبين الرسم مرة أخرى أن هناك 6 تباديل ممكنة.
طريقة التفكير الاستنتاجي:
يمكن أيضًا إيجاد عدد التباديل بوساطة التفكير الاستنتاجي. للخانة الأولى 3 خيارات محتملة هي أ، ب، جـ . ولكل من هذه الخيارات خياران آخران فقط لملء الخانة الثانية، بمجموع 3 × 2 = 6 خيارات. ومع كل واحد من هذه الاحتمالات الستة، يوجد خيار محتمل واحد للخانة الثالثة. أي بمجموع 6×1=6. ولذا فإن عدد احتمالات مجموعات الأحرف تساوي 3 × 2 × 1 = 6.واللجوء إلى الاستنتاج أفضل من مجرد حصر التباديل لأن التفكير الاستنتاجي يأخذ في الاعتبار كل الاحتمالات الممكنة، بينما قد يغفل أحدها أثناء الحصر، خاصة إذا كان لدينا عدد كبير من الأشياء.
لنفترض مثلاً أن لدينا 26 حرفـًـا بدلا من الأحرف الثلاثة أ ب جـ ، وطلب منا إيجاد إجمالي عدد المجموعات المحتملة والمكونة من 3 أحرف. نلاحظ أن حصر كل الاحتمالات صعب وممل بينما يمكن إيجاد الجواب بسهولة عن طريق التفكير الاستنتاجي. فكل احتمال من 26 خيارًا محتملاً يقع في الخانة الأولى يقابله 25 خيارًا في الخانة الثانية، وهذا يشكل ما مجموعه 650 احتمالا (26×25= 650). ولكل من هذه الـ 650 خيارًا، يتبقى 24 حرفـًا محتملاً لشغل الخانة الثالثة، أي ما مجموعه 15,600 تشكيل محتمل (650 × 24 = 15600). وبالتالي فعدد التباديل الإجمالي يساوي 26 × 25 × 24= 15,600.
يوضح المثال السابق قانون الضرب للتباديل : إذا كان يمكن ملء الخانة الأولى بـ ن من الطرق، ويمكن ملء الثانية بـ (ن - 1) من الطرق، والثالثة بـ (ن - 2) من الطرق، فإن عدد التباديل الإجمالي في الخانات الثلاث يساوي ن × (ن - 1) × (ن - 2).
لنفترض أن لدينا ما لايقل عن ثلاثة أحرف من كل من الحروف أ، ب، ج. كم مجموعة يمكن تشكيلها بحيث تتضمن كل مجموعة 3 أحرف ؟ (من هذه المجموعات أ أ أ، أ أ ب ، أ ب ب ...إلخ). في هذا المثال، يمكن ملء كل خانة بثلاث طرق مختلفة، وبالتالي يمكن حساب النتيجة : 3 × 3 × 3 = 27 مجموعة. وفي حالة وجود 26 حرفـًا بما لايقل عن ثلاثة من كل منها، فإنه يمكن تكوين 26 × 26 × 26 = 17,576 مجموعة.
استخدام الرموز والمعادلات:
رياضيـًا، يمثل الرمز نلر (أحيانـًا يكتب نلر) عدد تباديل ن من الأشياء مأخوذ ر منها في كل مرة. وباستخدام هذا الرمز يمكن صياغة الإجابة على مسائل التباديل على النحو :3 أشياء (مثل أ، ب، جـ ) مأخوذة 3 في كل مرة:
3 ل 3 = 3 × 2 × 1 = 6
26 شيئًا مأخوذة 3 من المرات:
26 ل 3 = 26 × 25 × 24 = 15,600
ن شيء مأخوذة ر من المرات:
ن ل ر = ن (ن-1) (ن-2) 000 [ن - (ر - 1)].
والصيغة الأخيرة هي الصورة العامة. أما المقدار الأخير [ن - (ر - 1)] فيعني ن مطروحـًا منها (ر-1)، وهو من الناحية الجبرية مساوٍ للمقدار (ن-ر+1). وهذا المقدار يعد بمثابة مؤشر يبين متى نتوقف عن كتابة عوامل الضرب المتتابعة في المعادلة. فمثلاً إذا كانت ن = 26، ر=3، فإن ( ن -ر +1) =26-3+1= 24، وبالتالي فـإن عوامل الضرب لـ 26ل3 هي 26 × 25 × 24.
حل مسائل التوافيق
إذا كان لديك 4 كتب، فكم مجموعة من 3 كتب يمكن تشكيلها ؟ هذا السؤال مكافئ للسؤال : ما عدد التوافيق الناتجة عن 4 أشياء مأخوذة 3 منها في كل مرة؟ لنفترض أن مؤلفي هذه الكتب علي التوالي هم: أحمد، بكر، جمال، داود. لو اخترنا الكتب المؤلفة من قبل أحمد، بكر وجمال، فإن المادة المقروءة ستكون نفسها بغض النظر عن ترتيب قراءة الكتب. ومن ثم فهناك توفيقة واحدة لهذه الكتب الثلاثة مأخوذ 3 في كل مرة. لكن ماعدد التوافيق الناتجة عن 3 كتب أخرى مأخوذة من الكتب الأربعة ؟ وكما في مسألة التباديل أعلاه، فإنه يمكن إيجاد الجواب عن طريق: 1- الحصر 2- التفكير الاستنتاجي 3- استخدام الصيغ الرياضية.
طريقة الحصر:
للتبسيط نمثل للكتب الأربعة بالأحرف أ ، ب ، جـ ، د. سجّل عدة مجموعات من هذه الأحرف الأربعة، ثم اشطب حرفـًا واحدًا في كل مرة مخلفـًا مجموعة من 3 أحرف. وفي كل مرة اشطب حرفًا مختلفـًا حتى تشكل المجموعات المتبقية توافيق مختلفة دائمـًا.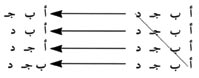 |
وهكذا تبين القائمة أن هناك 4 توافيق ممكنة.
طريقة التفكير الاستنتاجي:
خبرتنا بالتباديل ستمكننا من الوصول إلى الجواب على النحو التالي: هناك 6 طرق مختلفة لاختيار 3 كتب، ونرمز لها مثلاً بالرموز: أ ب جـ، أ جـ ب، ب أ جـ، ب جـ أ، جـ أ ب ، جـ ب أ، لكن هذه التشكيلات الست تمثل توفيقة واحدة. ومن هذا يمكن استنتاج أن هناك 6 تباديل لكل توفيقة مختلفة مكونة من 3 كتب. إذًا، فالعدد الإجمالي للتباديل يجب أن يساوي 6 أضعاف عدد التوافيق الممكنة. وبالمثل، فإن عدد التوافيق الممكنة يجب أن يساوي إجمالي عدد التباديل مقسومًا على 6. وأما مجموع تباديل 4 كتب مأخوذة 3 في كل مرة فهو:4 ل 3 = 4 × 3 × 2 = 24
وأما عدد التباديل لكل توفيقة من 3 كتب فهو :
3 ل 3 = 3 × 2 × 1 = 6
وإذًا، فعدد التوافيق الممكنة هو 24 - 6 = 4.
لنفترض أننا نرغب في إيجاد عدد توافيق 3 أحرف مختلفة يمكن اختيارها من 26 حرفـًا هي أحرف اللغة الإنجليزية. ولنتذكر مما سبق أنه عند حساب التباديل، وجدنا أن مجموع تباديل 26 حرفـًا مأخوذة 3 في كل مرة يساوي 26 × 25 × 24= 15,600. وكذلك وجدنا أن عدد التباديل لكل تشكيل توفيق من 3 أحرف هو 3 × 2× 1 = 6. وبالتالي فإن مجموع التوافيق الممكنة من الـ 26 حرفـًا هي 15,600 - 6 = 2,600.
طريقة الرموز والمعادلات:
يمثل الرمز نقر (أحيانـًا يكتب ( ) أو نقر عدد توافيق من الأشياء المأخوذة ر منها في كل مرة. وفي مثال الكتب الذي استعرضناه، يمكن صياغة وحساب عدد التوافيق الممكنة على النحو: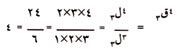 |
أما الصيغة العامة للتوافيق فهي:
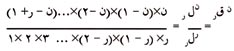 |
فمثلاً إذا كانت ن = 6، ر = 4، فإن:
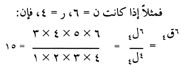 |
ويبسط الرياضيون صيغة ن ق ر باستخدام رمز المضروب للتعبير عن ضرب عدد كلي موجب في جميع الأعداد الكلية الموجبة التي تقل عنه. فمضروب 3 يعني 3 × 2 × 1، ويكتب 3! وبالمثل 4! يعني 4 × 3 × 2 × 1 وبالتالي يمكن تبسيط صيغة التباديل على النحو :
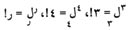 |
أما صيغة التوافيق المبسطة فهي:
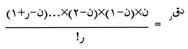 |
ويزيد علماء الرياضيات هذه الصيغة تبسيطـًا على النحو :
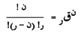 |
والصيغتان الأخيرتان متطابقتان لأن
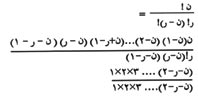 |
ويمكن اختصار جميع العوامل في هذه الصيغة عدا ن (ن - 1) (ن - 2) ... ( ن - ر + 1) في البسط و ر! في المقام. وهذه هي العوامل نفسها التي ظهرت في الصيغة الأصلية للتوافيق.
وبوساطة هاتين الصيغتين للتوافيق، يمكن حساب التوافيق المختلفة بطريقتين مختلفتين فمثلاً، إذا كان لدينا 5 كتب نختار منها مجموعة من 3، فيمكن حساب عدد التوافيق على النحو:
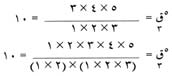 |
وعند اختصار العوامل المشتركة في البسط والمقام في الصيغتين أعلاه، سنجد أن الجوابين متطابقان.
★ تَصَفح أيضًا: العامل الحسابي.
نبذة تاريخية
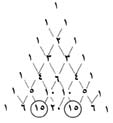 |
مثلث باسكال |
وقد وجد باسكال أن العنصر الواقع في الخانة (ر + 1) من الصف (ن + 1) هو عدد توافيق ن من الأشياء مأخوذة ر من المرات (ن قر). إذا كانت ن = 6، ر = 2، فإن عدد التوافيق هو العدد الواقع في الخانة الثالثة من الصف السابع (15)، (كما في داخل الدائرة) ولكن 15 تظهر أيضًا في الخانة الخامسة من الصف نفسه (★ تَصَفح الشكل). والسبب هو أن المثلث متماثل، وبالتالي فالعنصر الواقع في الخانة ر + 1 من الصف ن + 1 هو دائمًا العنصر نفسه الواقع في الخانة (ن - ر + 1) من الصف نفسه. وعليه فإن ن ق ر = ن ق (ن-ر) . وإذا كانت ن = 6، ر = 2 فإن العدد نفسه من التوافيق ممكن إذا أخذت الأشياء اثنين أو أربعة في كل مرة.