الإحصاء ( Statistics )

---

الإحصاء مجموعة الطرق الرياضية التي تستخدم لجمع وتحليل البيانات. وتساعد الطرق الإحصائية الناس على تحديد العديد من المسائل ودراستها وحلها. كما تتيح هذه الطرق اتخاذ القرارات المناسبة في مواجهة أوضاع قد يلفها الغموض وتفتقر إلى اليقين.

وتستخدم الطرق الإحصائية في مجالات مهن متعددة. فالأطباء يستخدمونها لتحديد مدى فاعلية بعض الأدوية في معالجة المشكلات الطبية. ويستخدمها رجال الأرصاد الجوية للحصول على تنبؤات أدق للطقس. ويستخدم المهندسون الإحصاء لوضع مواصفات ومقاييس معيارية للحصول على منجزات آمنة ومحكمة. وتساعد الخطط الإحصائية العلماء في تصميم التجارب العلمية. أما الاقتصاديون فإنهم يستعملون الطرق الإحصائية للتنبؤ بالأحوال الاقتصادية المستقبلية.

ويمكن استعمال المصطلح إحصاء إما اسمًا مفردًا أو جمعًا. فإذا استعمل في حالة الجمع فإنه يعني بيانات عددية. وإذا استعمل في حالة الإفراد فإنه يشير إلى مجموعة الطرق المستخدمة لجمع وتحليل البيانات. وتبحث هذه المقالة في الطرق الإحصائية.

استعمال الإحصاء لدراسة المشكلات

تتطلب الدراسة الإحصائية لمشكلة ما اتباع الخطوات الأربع الأساسية التالية على الأقل: 1- تعريف المشكلة 2- جمع البيانات 3- تحليل البيانات 4- عرض النتائج.

تعريف المشكلة:

يحتاج الإحصائيون إلى تعريف محدد لطبيعة المشكلة المراد بحثها وذلك بغرض الحصول على بيانات دقيقة بشأنها. فعلى سبيل المثال، إذا طُلب من إحصائي إجراء تعداد لسكان مدينة معينة في تاريخ معين، فإن عليه أن يعرف المعنى المراد بكلمة ساكن وذلك حتى يتمكن من تحديد الأشخاص الذين ينبغي أن يشملهم التعداد. فعلى الإحصائي مثلاً أن يقرر ما إذا كان حديثو الولادة في المستشفيات، والطلاب الموجودون بصفة مؤقتة بعيدًا عن كلياتهم ومدارسهم، والأشخاص الذين يقومون بزيارات طارئة للمدينة من أماكن أخرى، من السكان. فإذا لم يتمكن الإحصائي من تحديد المراد بالكلمة ساكن فإنه يصبح من الصعب عليه البدء في جمع البيانات المطلوبة.

جمع البيانات:

يحتاج المرء إلى معلومات متعددة وذلك فيما يختص بالمشكلات المختلفة. فالدراسة المتأنية لحالة بعينها مثل حادث تحطم طائرة، غالبًا ما تكون مفيدة. ولكن جمع البيانات عن الحوادث المشابهة سيقدم حتمًا معلومات يعتمد عليها في معرفة الأسباب الكامنة وراء الحادث.

إن تحديد الطرق التي ينبغي أن تُجمع بها البيانات المطلوبة إحدى أهم المهام التي يضطلع بها الإحصائي. ويمكن الحصول على بعض البيانات بصورة سهلة وقليلة التكاليف مثل قراءة مقياس الحرارة. ولكن، كثيرًا ما يلجأ الإحصائي إلى الاعتماد على عدد صغير من المشاهدات المختارة بعناية والمسماة عينة للحصول على المعلومات عن الكل.

ويجمع الإحصائيون البيانات ويأخذونها من مجتمع أو من عيّنة . ويتكون المجتمع من كامل المجموعة المتأثرة والمعنية بالمشكلة المراد دراستها، أما العيّنة فإنها جزء من المجتمع. ويستعمل الإحصائيون طرق الرصد والمشاهدة ويستعملون التجارب الضابطة (تجارب تجري للتأكد من صحة نتائج تجارب أخرى). وتتضمن طرق الرصد تسجيل المشاهدات عن الأحداث حال وقوعها بصورة طبيعية. ومن الأنواع الميسرة لدراسات الرصد ما يعرف بمسح العينة التي يسأل فيها الإحصائي عينة من المجتمع عن آرائهم الراهنة وظروفهم.

وعندما يستخدم الإحصائيون عينة فقط ؛ فإن عليهم التأكد من أن تلك العينة ستقدم لهم المعلومات التي يريدونها تمامًا. ويتطلب الأمر بالتالي قدرًا كبيرًا من التخطيط السليم المتأني. فعلى سبيل المثال، إذا طُلب من إحصائي، تقدير مستوى البطالة على المستوى القومي، فإنه يتعين عليه أن يحدد أولاً كيفية الحصول على عينة تمثل البلد بمجموعه بأدق صورة ممكنة. هل يجب أن تتضمن العينة العديد من الأسر في عدد قليل من المدن، أو يجب أن تتضمن عددًا أقل من الأسر في العديد من المدن؟

كثيرًا ما يقارن الإحصائيون بين مجموعات أو أفراد أو أشياء يختلف بعضها عن بعض بطريقة معينة، مثل مكان السكن أو الحالة الصحية. فمثلاً، قد يريد صانع أحد أنواع البسكويت أن يعرف ما إذا كان الناس في أنحاء مختلفة من البلد يستجيبون بطريقة مختلفة لمقدار حلاوة الطعام. ويتوقف نجاح عملية المقارنة عند مرحلة التحليل على قدرة الإحصائي على التحكم في الاختلافات المتعددة بين المجموعات. فلدراسة ما إذا كان الناس في الجنوب الشرقي من البلد مغرمين بأنواع البسكويت الأكثر حلاوة مقارنة بسكان الشمال، فإن الإحصائي يعمد للمقارنة بين الأطفال في الجنوب الشرقي وفي الشمال، وبين البالغين في منطقة معينة والبالغين في المنطقة الأخرى.

وتُمثل التجارب العشوائية الضابطة ، أكثر طرق جمع البيانات التي تتطلب قدرًا عاليًا من الدقة في الإعداد والتنفيذ، وهي أيضًا أكثرها ثراءً بالمعلومات المتطلبة لإجراء المقارنات. وفي هذا النوع من التجارب تقسم الأشياء قيد الدراسة، أو الناس المراد دراستهم إلى مجموعات مختلفة عشوائيًا، بهدف التحكم في تأثير الاختلافات التي لا يمكن قياسها.

وقد حدثت إحدى أهم التجارب العشوائية الضابطة في الخمسينيات من القرن العشرين، حينما جرى اختبار لقاح جديد كان الأطباء يأملون في استخدامه للوقاية من شلل الأطفال، إذ جرى اختباره على 400,000 طفل. وقد تلقى نصف عدد أطفال التجربة جرعات اللقاح، بينما تلقى النصف الآخر جرعات من محلول غير طبي يسمى بلاسيبو (الدواء الغُفل) ليس له أي مفعول على شلل الأطفال. وقد جرى اختيار الأطفال لكل من المجموعتين على أسس عشوائية. وكان لكل طفل فرصة متساوية ليكون في أي من مجموعتي اللقاح أو البلاسيبو. وكان من الواجب أن تتكون المجموعة الواحدة من عدد كبير من الأطفال بحكم أن نسبة الأطفال الذين يصابون بالشلل كانت منخفضة للغاية. وعليه فإن العينة الكبيرة وحدها هي التي تتيح معرفة مدى فاعلية اللقاح.

وقد قادت التجربة إلى نتائج باهرة. فقد تبين أن معدل الإصابة بالشلل في المجموعة التي تلقت البلاسيبو يبلغ ثلاثة أضعاف المعدل للمجموعة التي تلقت اللقاح. ونتيجة لذلك فقد خلص الإحصائيون والأطباء ممن قاموا بالتجربة، إلى أن اللقاح يساهم بفاعلية وجدوى في الوقاية من شلل الأطفال.

تحليل البيانات:

يقسم الإحصائيون الطرق التي يستخدمونها لتحليل البيانات إلى مجموعتين: 1- الطرق الاستكشافية 2- الطرق التأكيدية . وتستعمل الطرق الاستكشافية عادة للكشف عما يمكن أن تقدِّمه البيانات. وتتضمن هذه الطرق أحيانًا حساب المتوسطات أو النسب. وفي أحيان أخرى قد تستعمل الرسوم لعرض البيانات. أما الطرق التأكيدية فإنها تستعمل أسس نظرية الاحتمالات في محاولتها الإجابة عن أسئلة محددة. فعلى سبيل المثال، يمكن استخدام هذه الطرق للإجابة عن السؤال: هل سيؤدي تغيير لوحات السرعة القصوى على الطرق إلى تغيير السرعات التي يسير بها السائقون؟. تتطلب الطرق الإحصائية الحديثة، بشقيها الاستكشافي والتأكيدي، إجراء حسابات مكثفة، ويعتمد الإحصائيون على الحاسوب وعلى برامج معدة خصيصًا بغرض إجراء تحليلات متنوعة.

عرض النتائج:

يُعمم الإحصائي بوساطة الاستدلال النتائج التي توصل إليها من مجموعة مشاهدات قليلة العدد، أو من تجربة معينة، على المجتمع بمجموعه. وقد يجري عرض النتائج في صورة جدول، أو رسم بياني أو مجموعة من النسب. وبما أن الإحصائي قد قام باستعمال مجموعة صغيرة تمثل عينة وليس المجتمع بأكمله فإن النتائج المُقدمة لا بد أن تبرز قدرًا من عدم اليقين وذلك عبر استعمالها لتعابير الاحتمال وفترات القيم.

الاحتمال

في اللغة المتعارف عليها، تصف كلمة احتمال الأحداث التي لا تقع بصورة أكيدة. فنحن نتحدث عادة عن احتمال أن تهطل الأمطار غدًا، وعن احتمال أن تكون أداة كهربائية معينة تالفة، أو حتى عن احتمال وقوع الحرب النووية. وقد اجتهد الإحصائيون وعلماء الرياضيات لعدة قرون في وضع نظرية رياضية للاحتمال. وفي حقيقة الأمر، توصلوا إلى تطوير نظريات للاحتمال فالنظرية الشخصية تعبير عن درجة يقين الفرد حول وقوع حدث ما بغض النظر عن طبيعة ذلك الحدث. وتُطبق نظرية التكرار على الأحداث التي يمكن إعادة حدوثها مرة بعد أخرى، وذلك بصورة مستقلة وتحت ظروف متماثلة تمامًا.

ويمكن حساب النتائج المحتملة للأحداث باستعمال نظرية الاحتمال. فإذا افترضنا أنه جرى رمي قطعة نقود خمس مرات. فإن كل رمية سينتج عنها إما وجه الصورة أو وجه الكتابة. ويمكن اعتبار الحدثين متساويين في إمكانية الحدوث بما معناه أن احتمال أن تعطي قطعة النقود صورة، يبلغ النصف، وهو نفس احتمال أن تعطي الرمية كتابة. أما بالنسبة لمجموع الرميات الخمس، فإن هنالك 32 تسلسلاً محتملاً للصور والكتابة، على غرار صورة، صورة، صورة، كتابة، كتابة، أو كتابة، كتابة، صورة، صورة، كتابة. وهناك تسلسل واحد لن تظهر فيه صور فقط وهناك تسلسل واحد تظهر فيه صور فقط.

وبما أن كلاً من الـ 32 تسلسلاً متساوية الإمكانية فإنه يمكننا حساب عدد التسلسلات التي تقابل صفر صورة، وصورة واحدة، وهكذا، حيث نلاحظ أن احتمال عدد الصور هو:

عدد الصور صفر 1 2 3 4 5 الاحتمــالات 1/32 5/32 10/32 10/32 5/32 1/32

حتى نكوِّن فكرة جيدة عن الكيفية التي تكون عليها مجموعة الاحتمالات، يعرض الإحصائيون المعلومات دائمًا في شكل رسم بياني، يُعرف بتوزيع الاحتمالات . ويصبح توزيع الاحتمالات بالنسبة لمجموعة الاحتمالات، أعلاه، على النحو التالي:

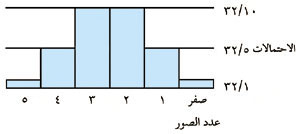توزيع الاحتمالات

عندما تقذف عملة معدنية لمرات عديدة، فإن احتمالات التوزيع بالنسبة لعدد الصور تقترب رويدًا رويدًا إلى المنحنى الذي يأخذ شكل الجرس، ويدعى التوزيع العادي .

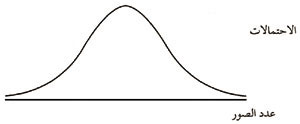التوزيع العادي

وتوضح النتائج المتحصل عليها من تجربة رمي القطعة المكررة مبدأ رياضيًا مهمًا هو نظرية النهاية المركزية . وتبعًا لهذه النظرية، فإن التوزيع الاحتمالي لمجموعات عدد كبير من الأحداث المكررة المستقلة بعضها عن بعض، يتم تقريبه بصورة جيدة بوساطة شكل التوزيع الطبيعي. وبسبب هذه العلاقة بين هذين التوزيعين، فإن التوزيع الطبيعي يمكن استعماله ليمثل التقريب وذلك للمساعدة في الاستدلال لعينة خاصة لإعطاء فكرة عن المجموعة كلها.

وتشترك كل التوزيعات الاحتمالية في عدد من الخصائص، فكل توزيع له متوسط أو متوسط قيمة . ويُحصل على هذا الرقم بضرب كل قيمة من التوزيع بالاحتمال المقابل لها ثم بأخذ المجموع لهذه المضروبات.

المتوسط= مجموع القيمة × احتمال القيمة

ويتم الحصول على متوسط عدد الصور المتحصل في مثال الرميات الخمس للعملة بوساطة العملية الحسابية التالية:

المتوسط= (صفر × 1/32) + (1 × 1/32) + (2 × 10/32) + (3 × 10/32) + ( 4 × 5/32) + (5 × 1/32) = ½ 2

وإذا رمينا القطعة بصورة متكررة لعدد من المرات يساوي (ن) وإذا كان احتمال الصورة هو ب، فإن متوسط عدد الصور هو ن × ب. وفي المثال أعلاه فإن ن = 5 و ب = ½ ، ويكون المتوسط بالتالي هو 5 × ½ أو ½ 2. وفي حالة التوزيع الطبيعي فإن المتوسط يتحقق عندما يبلغ المنحنى قمته.

ومن الخصائص المهمة الأخرى للتوزيعات الاحتمالية التباين والانحراف المعياري . ويقيس كلاهما انتشار القيم حول المتوسط. ويتم حساب التباين بناءً على المعادلة التالية:

التباين= مجموع [(القيمة - المتوسط)² × (احتمال القيمة)].

أما الانحراف المعياري فهو الجذر التربيعي للتباين. وفي حالة التوزيع الطبيعي، فإن احتمال أن تقع القيمة فيما بين انحراف معياري واحد من المتوسط هي، وفيما بين انحرافين حول المتوسط هي بالتقريب.

اختيار العينة

في مسح العينات والتجارب المتحكم فيها، يدرس الإحصائيون عينة مختارة من مجتمع أكبر. ويتم اختيار العينة البسيطة العشوائية بعملية يتوفر فيها لكل العينات المحتملة ذات الحجم الواحد، احتمال متماثل للاختيار. وفي حالة العينات العشوائية فإنه كلما كبر حجم العينة، ارتفعت درجة الوثوق بها في عملية تقدير كميات مثل المتوسطات أو النسب للمجتمع. وتُقاس درجة الوثوق بالعينة عادة بالانحراف المعياري لمتوسط العينة، ويتناقص الانحراف المعياري نسبيًا مع الجذر التربيعي لحجم العينة. وبناء على ذلك فإنه ولمضاعفة درجة الوثوق، يتعين على الإحصائي استعمال عينة أكبر حجمًا أربعة أضعاف.

وتختلف أحجام العينات كثيرًا اعتمادًا على الغرض من الدراسة الإحصائية. فمعظم دراسات الرأي العام المعروفة تضم عينات تحتوي على ما يتراوح بين 500 و 2,000 شخص. أما العينة المستخدمة لقياس معدل البطالة القومية الرسمي في الولايات المتحدة الأمريكية، فإنها تتضمن استبانة ما يربو على الـ 50,000 فرد. ويؤدي مثل هذا المسح إلى الحصول على متوسطات ونسب يعتمد عليها أكثر من خمس مرات مقارنةً بعيِّنة تستخدم 1,500 فرد فقط. وعلى الرغم من أنه قد تستعمل طرق معقدة من نظرية الاحتمالات لسحب العينات في هذه المسوحات، فإن معظم المسوحات تستخدم العينة البسيطة العشوائية لبنة أولى للبناء.

نبذة تاريخية

ترجع عملية جمع البيانات إلى الأزمان القديمة، ويشير الإنجيل إلى تفاصيل عدد من المسوحات الإحصائية. وقد وردت مادة أحصى ومشتقاتها إحدى عشرة مرة في كتاب الله عز وجل. وبدأ الإحصاء في الإسلام بأمر رسول الله ﷺ وقوله: (أحصوا لي كل من تلفظ بالإسلام ) أخرجه مسلم. وقد جمع القادة السياسيون والدينيون المعلومات عن الناس والممتلكات خلال العصور الوسطى في أوروبا وعصر النهضة الأوروبية. وفي القرن الثامن عشر الميلادي، جرى استعمال كلمة إحصاء في الجامعات الألمانية لوصف عملية إجراء مقارنات منظمة للبيانات الخاصة بالدول المختلفة.

وجرى تطوير كثير من الأفكار الإحصائية وطرق التحليل المستخدمة في عالم اليوم في أواخر القرن التاسع عشر الميلادي من قبل فرانسيس يزدرو أيدجورث وفرانسيس جالتون وكارل بيرسون وجورج أودني يول وعلماء آخرين وعلماء الرياضيات البريطانيين. وعلى الرغم من هذه التطورات، فقد بقي الكثير من الأفكار الإحصائية في صورته الأولية حتى عشرينيات القرن العشرين. وفي تلك الحقبة بدأ الكثير من الأفكار المتعلقة بالإحصاء ـ بوصفه فرعًا من فروع العلوم ـ في التبلور من خلال عمل مجموعة صغيرة من الإحصائيين العاملين أيضًا في إنجلترا. ويعود الفضل في ابتكار الاستدلال الإحصائي إلى كل من رونالد فيشر وجيرزي نيمان وإيجون بيرسون. وقد ابتكر فيشر أيضًا نظرية لتصميم التجارب تعتمد على التخصيص العشوائي للمعالجات، واقترح نيمان نظرية لمسوحات العينة بأفكار مشابهة مع تلك الواردة في نظرية تصميم التجارب.

وخلال الحرب العالمية الثانية (1939-1945م)، جرى الوصول إلى العديد من الأفكار الإحصائية وقد كانت جزءًا من المجهود الحربي في بريطانيا والولايات المتحدة. وفيما بعد الحرب، نما حقل الإحصاء واستخدمت الخطط الإحصائية في مجموعة متسعة من حقول المعرفة. وتستخدم الحكومات اليوم الإحصائيين على مختلف مستويات المسؤولية واتخاذ القرار. ويساهم الخبراء الإحصائيون في طرح الحلول المناسبة للعديد من المسائل المتعلقة بالبيئة والاقتصاد والنقل والصحة العامة والقضايا الأخرى. ويستعين القضاة والمحامون بصورة متزايدة بالإحصائيين لتقويم الأدلة والمقارنة بينها، ولتحديد مدى معقولية الشبهة. وتوظف الجامعات الإحصائيين للتدريس وإجراء البحوث، ويشتغل العديد من رجال الإحصاء بالعمل الاستشاري الخاص.