المحدد ( Determinant )

---

المُحدِّد في الرياضيات عدد واحد مرتبط بمجموعة مرتّبة من الأعداد المنظومة في شكل رباعي تُسمَّى العناصر. فعلى سبيل المثال، المجموعة المرتبة

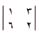مرتبطة بالعدد 16. ويمكن حساب قيمة هذا المحددّ باتباع الخطوات التالية: أولاً: نضرب العنصر العلوي الأيمن 3 في العنصر السفلي الأيسر 6 :3 × 6=18. ثانيًا: نضرب العنصر العلوي الأيسر 1 في العنصر السفلي الأيمن 2: 1 × 2 = 2 ، ثالثًا: نوجد حاصل طرح ناتج الخطوة الثانية من الخطوة الأولى: 18 - 2 = 16. وتستخدم كلمة محددّ أيضًا للتعبير عن المجموعة المرتبة نفسها.

ويستخدم علماء الرياضيات المحددّ لإيجاد صيغ حلول كثير من المسائل. وتشمل مسائل كهذه حلول معادلات وحساب مساحات وأحجام معينة.

استخدام محددات 2 × 2:

يطلق على المجموعة المرتّبة أعلاه مسمَّى محددّ 2 × 2، لأن لها صَفَّيْن هما (3، 1 و2، 6) وعمودين هما (3 ، 2 و 1 ، 6).

وعمومًا، يمكن استخدام الرموز أ ¡، ب ¡ ، أ ¢، ب ¢ للتعبير عن أعداد أي محدد 2×2. أما قيمة المحدد فهي على النحو التالي:

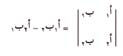ويمكن استخدام محدد 2×2 لحل المعادلات الخطية من مجهولين. وكمثال على ذلك، نفترض أننا نريد حل المعادلتين التاليتين:

3س + 1ص = 5
2س + 6ص = 14

لإيجاد قيمة المتغير س، نحذف المتغير ص عن طريق ضرب المعادلة الأولى في 6، ثم نطرح المعادلة الثانية منها:

ويمكن كتابة العمليات أعلاه على النحو التالي:

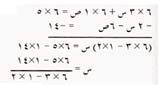ويمكن كتابة التعبير الجبري الأخير كنسبة بين محددين:

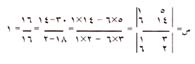وبالإمكان حل المعادلة الأصلية بطريقة مماثلة لإيجاد ص فنحصل على:

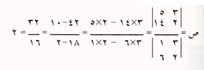لاحظ وجود نفس المحدد مقامًا في صيغتي كل من س و ص. يُسمّى هذا المحدد محدد النظام، ويتكّون من معاملات س ، ص في المعادلتين الأصليتين (3، 1، 2، 6). أما بسط صيغة س فهو نفس محدد النظام مع استبدال الثابتـين (5 ، 14) في المعادلتين الأصليتين بمعاملي س. وبالمثل، فإن هذين الثابتين يحلاّن محل معاملي ص في بسط صيغة ص.

وعمومًا، يمكن كتابة المعادلتين في س ، ص على النحو:

أ ¡ س + ب ¡ ص = حـ ¡
أ ¢ س + ب ¢ ص = حـ ¢

ويمكن حل هاتين المعادلتين لإيجاد س على النحو التالي: 1- اضرب المعادلة الأولى في ب ¢، 2- اضرب المعادلة الثانية في ب ¡، 3- اطرح ناتج الخطوة 2 من ناتج الخطوة 1 كي تحذف الحدود المحتوية على ص، وبالتالي تصبح النتيجة:

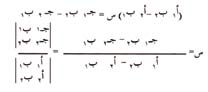استخدام محددات ذات رتب عليا:

رتبة المحددّ هي عدد الصفوف أو الأعمدة. فالمحدد 2×2 يعد من الرتبة الثانية. والمحدد 3×3 من الرتبة الثالثة، وهكذا. وتظهر المحددات ذات الرتب الأعلى من اثنين مثلاً، في حل ثلاث معادلات آنية أو أكثر.

وبالإمكان استخدام المحددات ذات الرتبة الثالثة لحل المعادلات الثلاث التالية:

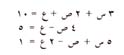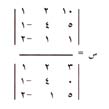
وتشبه صيغ إيجاد س ، ص ، ع تلك التي استخدمت لحل معادلتين فقط. فمقام كل صيغة هو محددّ النظام بينما البسط هو محددّ النظام مع استبدال الثوابت بمعاملات س، ص ، ع. فمثلاً صيغة س هي:

وهناك عدة طرق لحساب المحددّ من الرتبة الثالثة، مثل التي أعلاه، إحداها تكون باختزال المحددّ إلى سلسلة من المحددات ذات الرتبة الثانية. وبهذه الطريقة يمكن اختزال مقام الصيغة السابقة على النحو التالي:

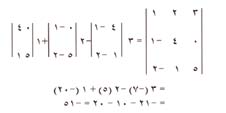في هذه العملية، يُضرب كل محددّ 2 × 2 في أحد عناصر الصف الأول (3 ، 2 ،1) من المحدد 3 × 3. وتُسمّى المحددات 2 × 2 بالمحددات الصغرى لعناصر الصف الأول. فمثلاً المحدد:

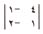هو المحدد الأصغر لـ 3، وتتكون من العناصر المتبقية في المحدد 3 × 3 بعد شطب الصف والعمود اللذين يحتويان على العدد 3. وبالمثل، فإن المحدد الأصغر لـ 2 يشمل العناصر المتبقية بعد شطب الصف الأول والعمود الثاني.

وتُسمَّى هذه السلسلة من المحددات 2 × 2 بعملية الفك بوساطة المحددات الصغرى للصف الأول، وتتكون من حاصل ضرب عناصر الصف الأول في المحددات الصغرى الخاصة بها. وتُحسَب قيمة المحدد 3 × 3 عن طريق تناوب جمع وطرح حواصل الضرب هذه. وعمومًا، فإن صيغة فك محدد 3 × 3 بهذه الطريقة هي:

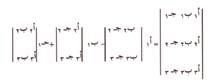ويمكن فك أي محددّ عن طريق المحددات الصغرى لأي صف أو عمود إذا ما تم اختيار الإشارات المناسبة لهذه المحددات الصغرى.

ويمكن أيضًا حساب المحددات ذات الرتبة الأعلى من الثالثة عن طريق اختزالها إلى محددات 2×2. ولكن المحددات الصغرى لهذه المحددات ليست من النوع 2×2. (فرتبة المحددّ الأصغر تقل دائمًا بواحد عن رتبة المحدد الذي تفرّعت منه).

ويلزم تكرار فك المحددات الصغرى حتى نحصل في النهاية على محددات 2 × 2. وقد يلجأ علماء الرياضيات إلى طرق أخرى لتبسيط المحددات ذات الرتب العليا.